- Verify Purchase
- Start Selling
- Blog
- Contact
- 0
Your cart is empty!
We continue our look at category theory with one more take on functors. So far, we have seen applications of category theory in implementing custom instances of the Expert trailing class, and the Expert Signal class so we will consider applications in using the Expert Money class for this article. All these classes come with the Meta Editor IDE and are used with the MQL5 wizard in assembling expert advisors with minimal coding.
Position sizing is one of the hot-button issues when it comes to trading system design. Results attained in the preliminary testing of any expert advisor are highly sensitive to it, it is often advisable to leave it out all together (use fixed margin or fixed lot size) or if you must to have it, add it at the very end when you already have a proper entry signal that is well balanced with your exit methods. That notwithstanding we are going to attempt to set an ideal position size based on a projected stop loss in a custom instance of the Expert money class.
Functors are a bridge between categories capturing the differences not just between the objects in each category but also the differences in their morphisms. We have been able to see how this captured information can be used to forecast changes in volatility and market trends when looking at categories that are in the form of graphs and linear-orders. Recall graphs and linear-orders are not categories per se but were viewed as such because key category axioms were present.
Functors had been implemented using simple linear equations in articles 14 and 15 where the mapping simply required a coefficient for slope and a y intercept to determine codomain-category objects and morphisms. Since article 16 we have started looking at functors as a simple neural network called a multi-layer perceptron. This network that stemmed from the work of Warren Sturgis McCulloch and Walter Pitts and has been shown to approximate any continuous function from -1 to +1 has also been known for some time to replicate any XOR function if it is multi-layer.
In this article as we sum up our look at functors we’ll examine how when paired with monoids and a pre-order of security prices, we can formulate a system to set position sizes when trading the a security, which will be BTCUSD (bitcoin). When we last looked at monoids, their principle application to traders came in classifying trading steps so that decisions could be made by the operations of each monoid. Recall a monoid is a set, a binary operation and an identity element. We had therefore created monoids for each of the notional steps a trader faces when making decisions on opening a position.
If we make a quick recap of some fundamentals covered so far, objects (referred to in earlier articles as domains) are the cell or building block of categories. Within a category objects have mappings with each other that are called morphisms and in the same way that you have morphisms linking objects, so do functors link categories.
So, the linkage between categories provided by functors has been useful in making forecasts since the codomain category has been a time series whose forecast is our subject. In our last article this was informing the decision whether we go long or short on the S&P 500.
However unlike in the last article where functors were linking graphs to linear-orders, we will have monoids as the domain category. As mentioned we used monoids as decision points at each step taken in making a trade. These steps which are bound to differ from what other traders use because of differences in strategy, were selecting a timeframe, selecting a lookback period, selecting an applied price to use, selecting an indicator that incorporates the afore chosen timeframe, lookback, and applied price in producing a reading. The final selection was for trade action, that is whether given the indicator value, we follow its trend or position counter to its value. So, the monoids were coded for each of these decisions and the binary operation of each monoid was responsible for selecting the appropriate value from each set, after iterating through all the set values.
Multi-layer’s perceptron’s role in trading cannot be overstated. The sheer volume of related articles on neural networks all serve as a clear testament to why they have been and are increasingly becoming indispensable. For most traders though, their use is in projecting next price trends for a security, which is fine. What may be overlooked though, in my opinion, is in selecting (and perhaps regularizing) the input data for the network. Yes, you want to forecast a time series but what data stream will you base your projection on and why? This may sound trivial but it could be why many networks that are trained on sizeable amounts of data do not perform as they did on test runs, amongst other factors.
So as we had used monoids in informing decisions at each of the steps we had in our very basic trade system for article 9, and a few others like it that followed, we will do the same for this article with only exception being the final step will be omitted leaving four steps. The omitted fifth step whose monoid set whether to follow the trend or trade counter to the trend is not relevant here. Our Multi-Layer Perceptron (MLP) will then use each of the four remaining monoid output values as inputs. The target output for which our MLP will be trained will be the ideal stop loss points for an open position. The size of this stop loss gap is inversely proportional to the lots traded in a position therefore it will serve as a key metric of our position size.
So, this is how we will come up with a position size based on projected stop loss gap:
//output from MLP forecast double _stoploss_gap=_y_output[0]; //printf(__FUNCSIG__+" ct call: "+DoubleToString(_stoploss_gap)); sl=m_symbol.Ask()+fabs(_stoploss_gap); //--- select lot size double _ct_1_lot_loss=(_stoploss_gap/m_symbol.TickSize())*m_symbol.TickValue(); double lot=((m_percent/100.0)*m_account.FreeMargin())/_ct_1_lot_loss; //--- calculate margin requirements for 1 lot if(m_account.FreeMarginCheck(m_symbol.Name(),ORDER_TYPE_SELL,lot,m_symbol.Bid())<0.0) { printf(__FUNCSIG__" insufficient margin for sl lot! "); lot=m_account.MaxLotCheck(m_symbol.Name(),ORDER_TYPE_SELL,m_symbol.Bid(),m_percent); } //--- return trading volume return(Optimize(lot));
First, we compute the lot loss or dollar value in drawdown incurred when a position of one lot is open in the red over the projected stop loss gap. This is the gap divided by tick size times tick value. If we take ‘m_percent’ the percentage allocation of margin typically allotted to a new position, to be the maximum allowable percentage drawdown for the position to be opened, then our lots will be that percentage divided by 100, multiplied by our free margin, and divided by the lot loss. In other words, how many single lot losses can we sustain in our maximum drawdown amount?
So, the coding for making decisions of each monoid as per previous articles was handled by one function, the ‘Operate’ function and depending on the operation method for the input monoid, it involved making a selection from the monoid set’s values. Operation methods used in our case were very rudimentary, numbering 6 of which we only used 4 since addition and multiplication required zero and one to always be present in the monoid sets which was not possible in our case. Our code highlighting this enumeration and the function is as follows:
//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations | //+------------------------------------------------------------------+ enum EOperations { OP_FURTHEST=5, OP_CLOSEST=4, OP_MOST=3, OP_LEAST=2, OP_MULTIPLY=1, OP_ADD=0 };
//+------------------------------------------------------------------+ //| Operate function for executing monoid binary operations | //+------------------------------------------------------------------+ void CMoneyCT::Operate(CMonoid<double> &M,EOperations &O,int IdenityIndex,int &OutputIndex) { OutputIndex=-1; // double _values[]; ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0); // for(int i=0;i<M.Cardinality();i++) { m_element.Let(); if(M.Get(i,m_element)) { if(!m_element.Get(0,_values[i])) { printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1)); } } else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); } } // if(O==OP_LEAST) { ... } else if(O==OP_MOST) { ... } else if(O==OP_CLOSEST) { ... } else if(O==OP_FURTHEST) { ... } }
Now because we are now interested in position sizing and not volatility of market trend forecasting, the final ‘action’ monoid and its decision can be replaced by a functor. So, the first four monoids will be executed to help in deciding the indicator reading to guide in position sizing. We’ll stick with RSI and Bollinger bands indicators with the later regularized as before to yield a value like the RSI that is between 0 and 100. So, even though this indicator reading is the result of three earlier monoid results, it will be paired with them to create a set of four values that form the inputs of our multi-layer perceptron. The inputs of timeframe and applied price will therefore need to be regularized as we did in the last article to a numeric format that can be processed by the MLP.
So, to reiterate a monoid which is simply a set, a binary operation and an identity element, simply allows selection of an element from that set as defined by the binary operation. By selecting a timeframe, lookback period and applied price we are getting the inputs for our indicator whose normalized value (0-100) will serve as the fourth input in the MLP.
The step details involved in selecting the timeframe, lookback period, applied price and indicator to use were covered in an earlier article and their updated code is attached. Nonetheless below is how the outputs from each of the respective functions is got:
ENUM_TIMEFRAMES _timeframe_0=SetTimeframe(m_timeframe,0); int _lookback_0=SetLookback(m_lookback,_timeframe_0,0); ENUM_APPLIED_PRICE _appliedprice_0=SetAppliedprice(m_appliedprice,_timeframe_0,_lookback_0,0); double _indicator_0=SetIndicator(_timeframe_0,_lookback_0,_appliedprice_0,0);
To properly harness our MLP we need to train it aptly. In the last article training was done at initialization and the most profitable network’s weights, if available for the chosen network setting, were loaded and used as the starting point of the training process in adjusting the weights. For this article no pre-training is performed before or at initialization. Instead, with each new bar, the network gets trained. One bar at a time. This is not to suggest it is the right approach but rather it is simply an exhibition of the many options one has when it comes to training an MLP or network for that matter. The implication of this though is that because initial weights are always random, the same expert settings are bound to yield very different results on different test runs. As a work around this, a profitable test run will have its weights written to a file and on the start of the next run with similar network settings (number of items in hidden layer) these weights will be loaded and will serve as the initial weights on a test run. The network read and write functions remain proprietary and so only reference to their library is presented here as the reader is meant to implement his own.
So, the synergy of monoids and MLP is what is really presented here since it can be argued that either on their own can come up with stop distance forecasts. This would ideally require a control, for verification, meaning we would need to have separate expert advisors that implement only monoids, and only MLPs and compare all three sets of results. This unfortunately is not feasible for this article however the source code showing both ideas so attached so the reader is invited to explore and verify (or refute?) this idea of synergy.
So, the code integrating the two is listed as follows:
m_open.Refresh(-1); m_high.Refresh(-1); m_close.Refresh(-1); CMLPTrain _train; int _info=0; CMLPReport _report; CMatrixDouble _xy;_xy.Resize(1,__INPUTS+__OUTPUTS); _xy[0].Set(0,RegularizeTimeframe(_timeframe_1)); _xy[0].Set(1,_lookback_1); _xy[0].Set(2,RegularizeAppliedprice(_appliedprice_1)); _xy[0].Set(3,_indicator_1); // int _x=StartIndex()+1; double _sl_1=m_high.GetData(_x)-m_low.GetData(_x); if(m_open.GetData(_x)>m_close.GetData(_x)) { _sl_1=m_high.GetData(_x)-m_open.GetData(_x); } double _stops=(2.0*(m_symbol.Ask()-m_symbol.Bid()))+((m_symbol.StopsLevel()+m_symbol.FreezeLevel())*m_symbol.Point()); _xy[0].Set(__INPUTS,fmax(_stops,_sl_1)); _train.MLPTrainLM(m_mlp,_xy,1,m_decay,m_restarts,_info,_report);
To analyze our composite position sizing method, we will use bitcoin (BTCUSD) as the test security. Testing by optimization will be done from 2020 1st January to 2023 1st August on the daily time frame. Besides optimizing for the ideal number of weights in the hidden layer since we are using an MLP with only one hidden layer, we will also look to fine tune the four monoids we are using in getting the position size. This means we will look to set the ideal identity element and operation type for each of the four monoids used in coming up with our position size. Our analysis is focused squarely on position sizing meaning the expert signal used will have to be one of those provided in the MQL5 library. For this we will use RSI expert signal class. No trailing stops will be implemented and as always as have been doing in all the previous tests no take profit or stop loss values will be used so the parameters for ‘take level’ and ‘stop level’ will be zero. Our expert will be open to the possibility of using pending orders though and so the parameter ‘price level’ will also be optimized as before.
We perform tests with the objects functor and with the morphisms functor. The results of which are presented below respectively:
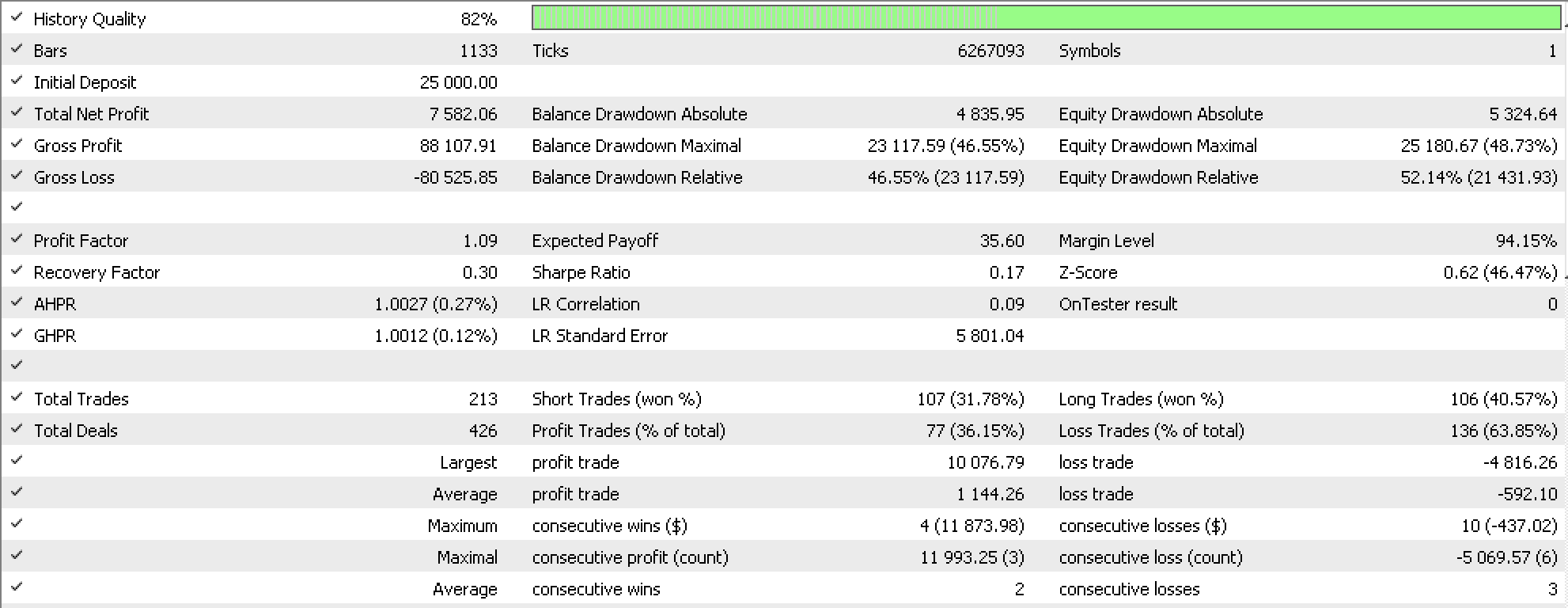
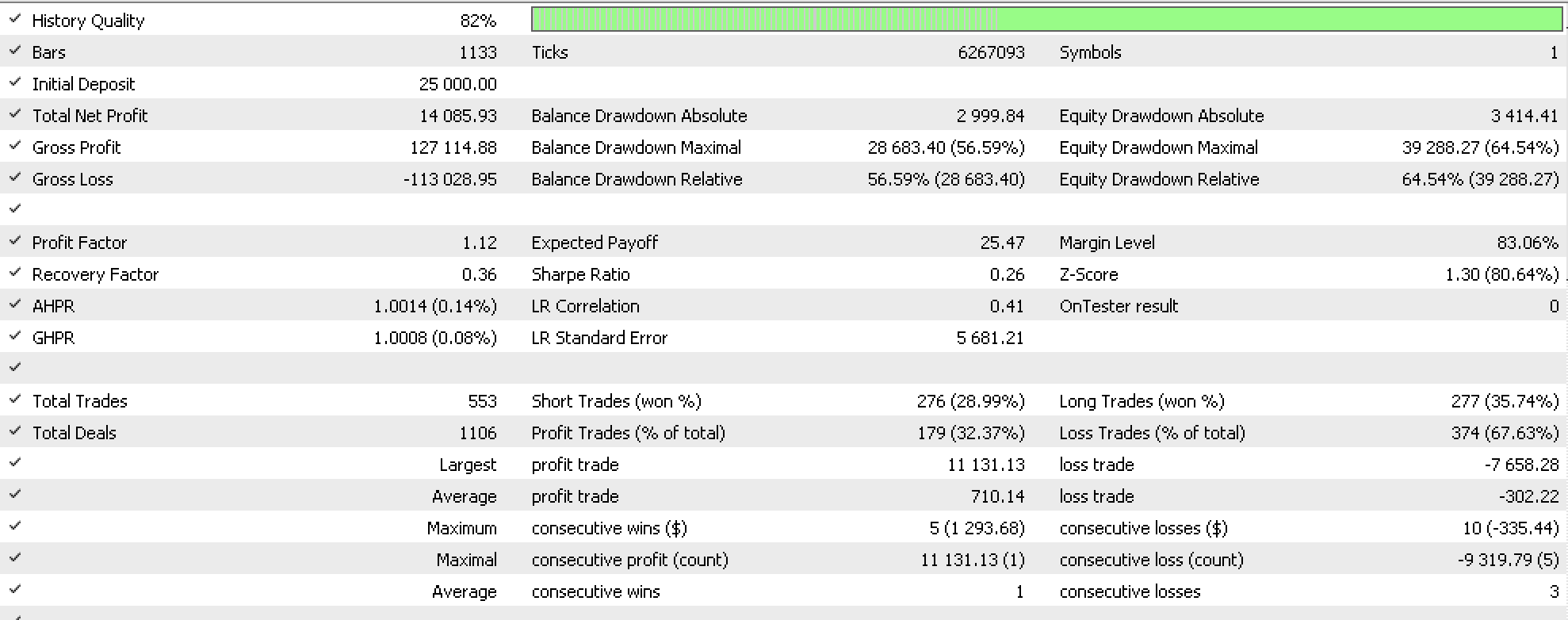
For any given input values such as these from the run with object morphisms above, the results are not necessarily reproducible because on initialization of each MLP, random weights are assigned. Now it does help that we can load weights from a prior profitable run when initializing to avoid starting from zero every time, but even then, because training is on each new bar, you would end up adjusting the weights of the profitable MLP meaning you would not get identical results. This therefore calls on the reader to code a method custom to his strategy, that carefully logs and reads the weights from his best test runs.
If as a control we run an expert advisor with the same RSI signal, same no trailing stop but with a different position sizing method, of using a fixed margin, we do get the results below:
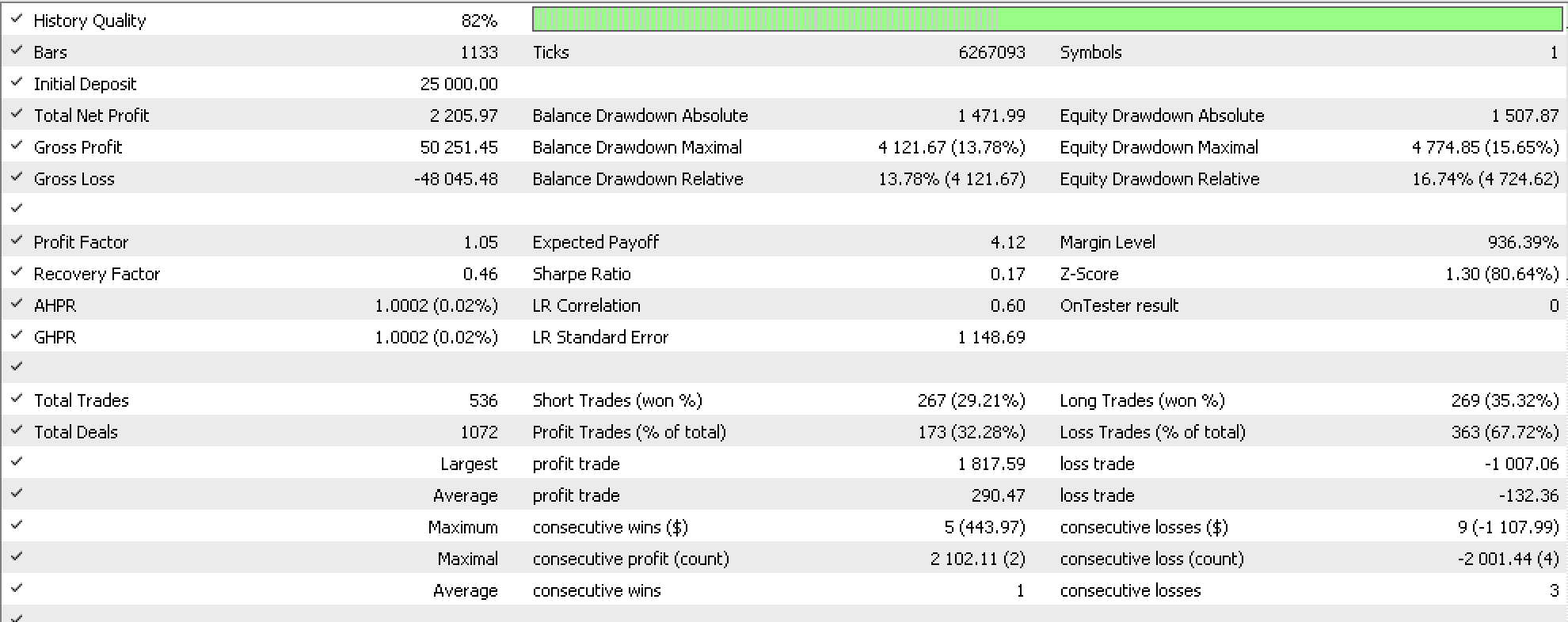
From the results our systems tended to yield better results even without exhaustive test runs. (Optimizations were cut short as the purpose was only to show potential). However as stated at the onset of the article, usually, for most traders the positions sizing aspects of the system are what you tinker with last, if at all, as they have a huge influence on the test run results and would strictly speaking mean nothing if a solid entry signal is employed with the system.
Potential challenges and limitations from our functor-based position sizing are covered by a continuum of points, let’s try to highlight a few. Firstly, for any trader, we need to appreciate there is a steep learning curve involved in getting monoid sets that work with his strategy and establishing appropriate MLP training patterns. Both of these are crucial in implementing the strategy presented here and they will require a decent amount of time is invested before arriving at works.
Secondly price gaps or securities whose one-minute OHLC data is inconsistent with its real tick data will not yield dependable monoid settings or MLP weights when traded on a live account (given a forward walk). The reasons are obvious but this is a major sticking point when it comes to implementing the ideas presented here.
Thirdly over fitting and generalization is another problem that specifically plagues MLPs. I hinted at this earlier by noting on importance of input layer data set, and the work around this in my opinion is using meaningful data that is regularized. ‘Meaningful’ in the sense that there are credible fundamental aspects of the input layer dataset that one would expect to affect the forecast we are interested in.
And then there is the problem of parameter tuning, which some may say ties in with the previous point, but I would argue it goes beyond that if we consider the cost of the CPU resources involved and the amount of time in arriving at our target parameters then it is clearly a problem that is beyond over fitting.
Poor interpretability and transparency of any systems developed using MLPs is another hurdle that coders need to be aware of. If you have a system that works and you want to start attracting investors, often they require you disclose more on how your system works thanks to its MLP. This could present a challenge depending on your network’s layers and its complexity, in convincing your potential suitors. There are other aspects as well like data-preprocessing which is sort of mandatory for MLPs as they always need to load weights, market regime changes, and model updating and maintenance and so on. All these factors need to be considered and appropriate contingencies developed to address them, as and when they manifest.
In fact, it may be argued that the last points on market regime change make the case for traditional trading approaches like manual trading. I believe the jury is still out on that as today systems are being developed and tested across extensive history data sets that capture a wide range of market regimes.
To summarize our key takeaways and findings from this study, we’ve shown how a different perspective on a monoid, as a category can be implemented in the MQL5 language. We’ve gone further to demonstrate that this implementation can be useful in guiding the position size of a trade system, that in our case relied on the RSI indicator for entry and exit signals.
The significance of functors and monoids being used as position sizing tools does imply that the same can be done for other aspects of a trading system such as entry signal or as has often been the case in these series trailing stop placement & adjustment.
As noted at the end there is still some work and hurdles to be overcome before traders can fully utilize ideas presented here so readers are invited to explore and experiment with functor based approaches in developing their trading systems.
Relevant sources are from Wikipedia as per the hyperlinks in the article.
Do place the files MoneyCT_17_.mqh' in the folder 'MQL5\include\Expert\Money\' and 'ct_9.mqh' can be in the include folder.
You may want to follow thisguideon how to assemble an Expert Advisor using the wizard since you would need to assemble them as part of an Expert Advisor. As stated in the article I used the RSI oscillator as the entry signal and no trailing stop. As always, the goal of the article is not to present you with a Grail but rather an idea which you can customize to your own strategy. The *.*mq5 files that are attached are what was assembled by the Wizard, you may compile them or assemble your own. The file underscored 'control' was assembled with fixed margin position sizing.