- Verify Purchase
- Start Selling
- Blog
- Contact
- 0
Your cart is empty!
The cuckoo is a fascinating bird, not only because of its singing, but also because of its aggressive breeding strategy, which consists in laying eggs into nests of other birds. Thus, the bird completely shifts its parental responsibilities to other species. Each cuckoo species lays eggs of a certain color and size in order to best match the eggs of various foster parents. Cuckoo chicks thrown into other birds' nests are usually larger and stronger than the nest owners' own chicks, so cuckoos need more food. During development, Hodgson's cuckoo chicks develop a special pattern on their wings in the form of an open beak, which allows them to receive more food from foster parents. The cuckoo is not the only bird demonstrating such a trait. Nesting parasitism has been found in at least 80 species of birds. Also, this phenomenon is widespread in some species of social insects - bumblebees, bees and ants whose females penetrate into another colony, kill the queen and lay their eggs. Nesting parasitism also exists among some fish, such as catfish from the Lake Tanganyika in Africa, which throw in their eggs to other fish incubating eggs in their mouths.
Cuckoo search is one of the latest nature-inspired heuristic algorithms developed by Yang and Deb in 2009. It is based on the parasitism of some cuckoo species. This algorithm has been further improved by so-called Levy flights rather than simple isotropic random walk methods.
The Cuckoo Optimization Algorithm (COA) is used for continuous non-linear optimization. COA is inspired by the lifestyle of this bird. The optimization algorithm is based on the features of the species' egg-laying and reproduction. Like other evolutionary approaches, COA starts with an initial population. The basis of the algorithm is an attempt to survive. While competing for survival, some of the birds die. Surviving cuckoos move to better places and begin to breed and lay eggs. Finally, the surviving cuckoos converge in such a way that a cuckoo society with similar fitness values is obtained.
The main advantage of this method is its simplicity: cuckoo search requires only four understandable parameters, so tuning becomes a no-brainer.
In the cuckoo search algorithm, the eggs in the nest are interpreted as possible solutions to the optimization problem, and the cuckoo egg represents the new solution. The ultimate goal of the method is to use these new (and potentially better) parasitic cuckoo egg solutions to replace the current nest egg solution. This replacement, carried out iteratively, eventually leads to a solution.
Professors Yang and Deb proposed the following three sets of ideal states for the algorithm:
1. Each cuckoo lays one egg and drops it into a randomly selected nest.
2. The best nests with high quality eggs will be passed on to the next generations.
3. The number of available nests is fixed, and the nest can detect an alien egg with the 'pa' probability. In this case, the host bird can either throw away the egg or leave the nest and the egg will die.
For simplicity, the third assumption can be approximated by the pa fraction of n nests. For the maximization problem, the quality or appropriateness of the solution may simply be proportional to the objective function. However, other (more complex) expressions for the fitness function can be defined as well.
For each iteration g, a cuckoo egg i is randomly selected and new solutions xi (g + 1) are generated using Levy flight, a kind of random walk in which the steps are determined within bounds of step lengths that have a certain probability distribution, and the directions of the steps are isotropic and random. According to the original creators of the method, the strategy of using Levy flights is preferable to other simple random walks because it results in better overall performance. The general Levy flight equation looks as follows
xi(g + 1) = xi(g) + α ⊕ levy(λ),
where g indicates the number of the current generation, while α > 0 indicates the step size, which should be related to the scale of the particular problem under study. The ⊕ symbol is used to denote element-wise multiplication. Note that this is essentially a Markov chain, since the next location in generation g + 1 depends only on the current location in the g generation and the transition probability given by the first and second terms, respectively. This transition probability is modulated by the Levy distribution as:
levy(λ) ∼ g−λ, (1 < λ ≤ 3),
which has infinite variance with infinite mean. Practice has shown that the best results are achieved with a fixed degree of 2.0. Here, the steps essentially form a random walk process with a power-law heavy-tailed step length distribution. From the computational point of view, the generation of random numbers using Levy flights consists of two stages: first, a random direction is chosen according to a uniform distribution, then steps are generated according to the chosen Levy distribution. The algorithm then evaluates the suitability of the new solution and compares it with the current one. In case the new solution provides better suitability, it replaces the current one. On the other hand, some nests are abandoned (the owner of the nest threw out the cuckoo egg or left the nest and the egg died) in order to increase the exploration of the search space in search of more promising solutions. The replacement rate is determined by the pa probability, a model parameter that needs to be tuned to improve performance. The algorithm is applied iteratively until the stopping criterion is met. Common termination criteria are that a solution has been found that satisfies a lower threshold, a fixed number of generations has been reached, or that successive iterations no longer produce better results.
Let us dwell in more detail on the process of laying eggs by the cuckoo. From all the nests, a nest where the egg is supposed to be laid will be randomly selected. Since the egg is a solution, it can be represented by the quality of the egg. If the cuckoo egg is of higher quality than the parent egg, then it will be replaced. Otherwise, the parent egg will remain in the nest. In fact, subsequent evolution will continue from the surviving chick. This means that if the chick of the parent egg survived, then evolution will continue from the same place. Further development is possible only if the cuckoo egg turns out to be more viable and the search for solving the problem continues from a new place. The decision tree is schematically shown in Figure 1.
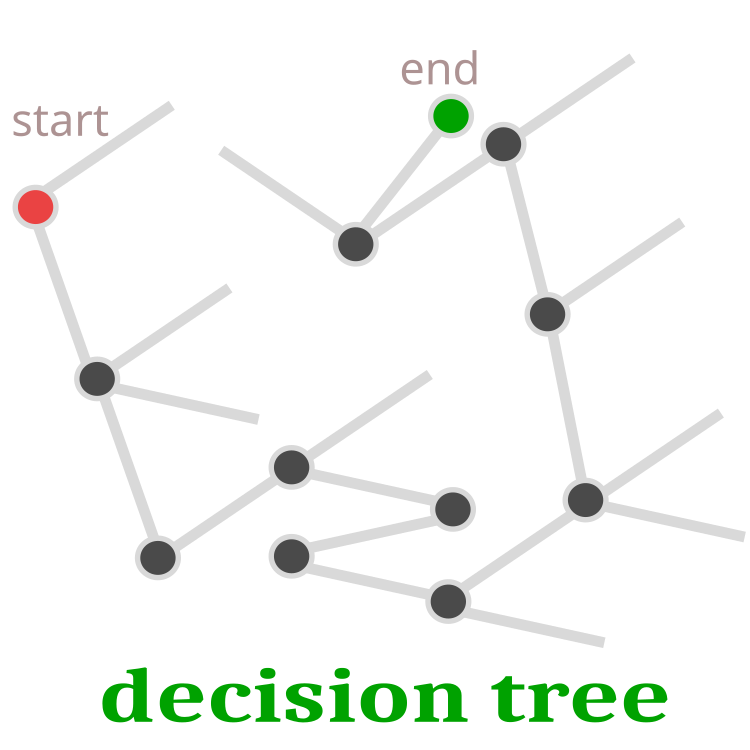
Fig. 1. Decision tree. The red dot is the beginning, the green dot is the final decision
The second component of the basis of the algorithm after the decision tree is Levy flight. Levy flight is a random walk (a Markov statistical process) in which the length of the jump changes in steps, the direction of the jumps changes randomly, and the probability distribution is a special case of the Pareto distribution and is characterized by heavy tails. It is defined as a jump in space, and the jump is isotropic in random directions. Levy flight is a tool for describing anomalous stochastic processes. The dispersion is infinite (jumps of great length are possible), the lengths of the jumps are self-similar at all levels (short jumps are interspersed with long flights). The term Levy flight is sometimes extended to include a random walk that occurs on a discrete grid rather than in a continuous space.
A clear application of Levy flight in the cuckoo algorithm can be imagined if we consider an optimization problem with one parameter. Let's take a hypothetical function (the black line in Figure 2), which does not change over most of its domain of definition, i.e. horizontal line (y=x). Only in a small area, the function changes and has one maximum. If we start the search for the maximum from the orange dot in Figure 2, then getting a random value x with the Levy distribution, we will move away from the starting point, while not getting a change in the function. However, with a strong jump in the tail of the distribution, we get a green dot, which is a better solution than the original orange one, and then only from the green dot we can improve the result, while approaching the maximum of the function. In this example, Levy flight dramatically improves the search capability of the algorithm.
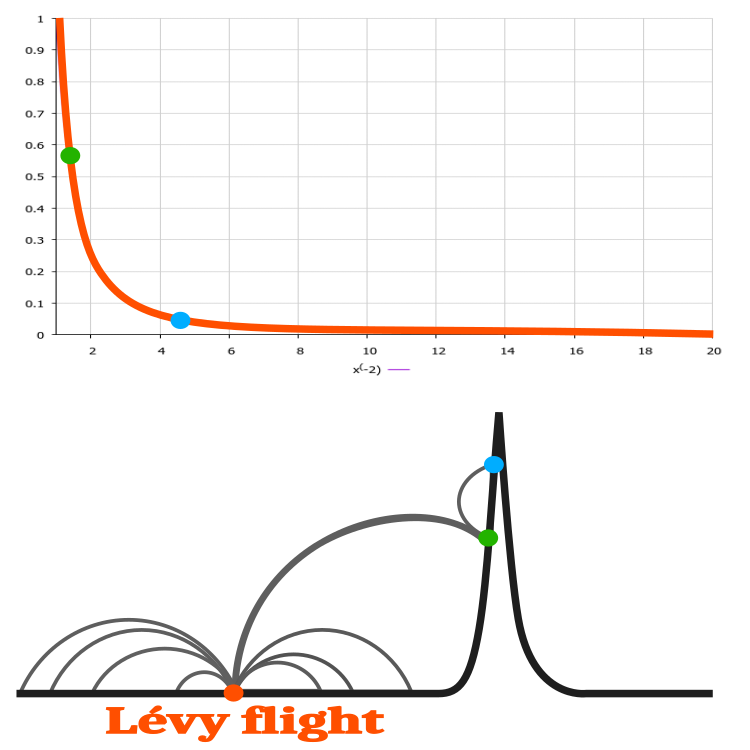
Fig 2. An example of finding a solution to a hypothetical one-dimensional function using the Levy flight
The concept of Levy flights is used in chaos theory, when modeling random or pseudo-random natural phenomena (for example, the flight of an albatross, combining long and short trajectories). Examples include earthquake data analysis, financial mathematics, cryptography, signal analysis, turbulent motion, as well as many applications in astronomy, biology and physics.
COA algorithm pseudo code (Figure 3):
1. Initialization cuckoos with random values.
2. Defining fitness.
3. Laying eggs in random nests.
4. Empty the nest with a given probability.
5. Send cuckoos from the current position to a random direction within the Levi flight distance
6. Defining fitness.
7. Laying eggs in random nests.
8. Empty the nest with a given probability.
9. Repeat p. 5 until the stop criterion is met.
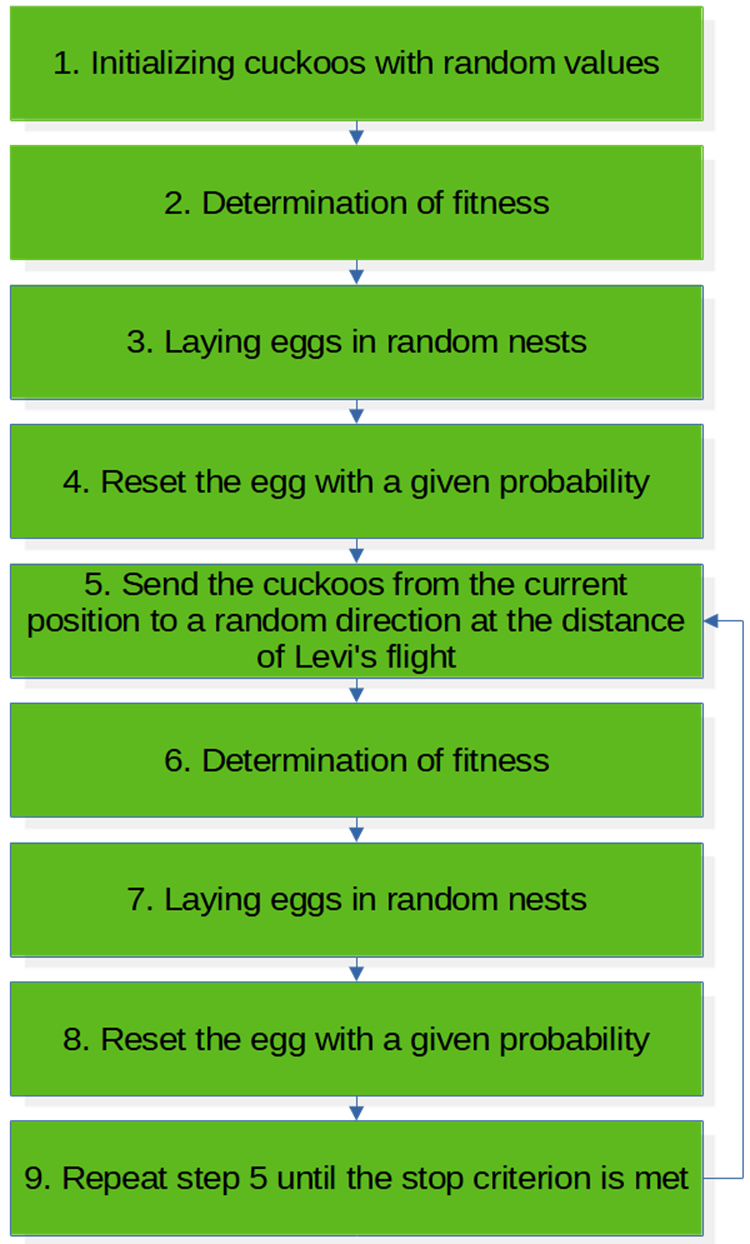
Fig. 3. COA algorithm block diagram
Let's start considering the code of the algorithm. The solution to the problem is the cuckoo, which is also the egg. This is a simple structure that includes the coordinates in the search space and the value of the fitness function (egg quality).
//—————————————————————————————————————————————————————————————————————————————— struct S_Cuckoo { double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Let's describe the nest in the form of a structure. Here, just like in the structure of an egg, there are coordinates in space and the value of the fitness function. "Laying the egg in the nest" essentially means copying the structure of the egg into the structure of the nest. When using the pa probabilistic parameter, the egg is ejected from the nest when a random number from 0.0 to pa falls out in the range [0.0;1.0] and the value of e is set equal to -DBL_MAX.
//—————————————————————————————————————————————————————————————————————————————— struct S_Nest { void Init (int coordinates) { ArrayResize (c, coordinates); e = -DBL_MAX; } double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Algorithm class. The public initialization methods, the main two methods of calling in the user program, the ranges of values of the arguments of the optimization problem and additional private methods that perform service functions are declared here.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Cuckoo cuckoos []; //all the cuckoos public: double cB []; //best coordinates (egg parameters) public: double eB; //best eggs quality public: void Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP); //step control value public: void CuckooFlight (); public: void LayEggs (); //============================================================================ private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: S_Nest nests []; //nests private: int cuckoosNumber; //number of cuckoos private: int nestsNumber; //number of cuckoo nests private: double koef_pa; //probability of detection of cuckoo eggs private: double koef_alpha; //step control value private: double v []; private: int coordinates; //coordinates number private: bool clutchEggs; //clutch of eggs }; //——————————————————————————————————————————————————————————————————————————————
Init () public method. Here, the values of variables are reset and memory is allocated for arrays.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP) //step control value { MathSrand (GetTickCount ()); clutchEggs = false; eB = -DBL_MAX; coordinates = coordinatesP; cuckoosNumber = cuckoosP; nestsNumber = nestsP; koef_pa = koef_paP; koef_alpha = koef_alphaP; ArrayResize (nests, nestsNumber); for (int i = 0; i < nestsNumber; i++) { nests [i].Init (coordinates); } ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (v, coordinates); ArrayResize (cuckoos, cuckoosNumber); for (int i = 0; i < cuckoosNumber; i++) { ArrayResize (cuckoos [i].c, coordinates); } } //——————————————————————————————————————————————————————————————————————————————
The first public method called on each iteration of the "cuckoo flight". If the clutchEggs flag is off, then we send the cuckoos in a random direction, generating random numbers in the range of the corresponding coordinate. If the flag is enabled, then the actual flight of the cuckoo is carried out according to the distribution of the Levy flight in the range of the v vector. The v vector is pre-calculated in Init () for each coordinate separately, since each coordinate may have a different range of values.
The cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); expression means that we add the offset r1 * v [c] * pow (r2, -2.0), where r1 is -1 or 1, which determines the direction of the offset from the original position, v is a displacement vector, r2 is a random number in the range from 0.0 to 20.0 raised to power -2.0. Raising a random number to a power is the Levy flight function. Its graph can be seen in Figure 2.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::CuckooFlight () { //---------------------------------------------------------------------------- if (!clutchEggs) { for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } clutchEggs = true; } else { double r1 = 0.0; double r2 = 0.0; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
The second public method called on each iteration is "laying eggs". In this method, the simulation of laying a cuckoo egg in a nest is algorithmically reproduced. This happens by choosing a random nest from all existing ones. After that, there is a comparison of the cuckoo egg quality and the one that is already in the nest. If the cuckoo egg is better, then a replacement takes place. An interesting feature of the algorithm in this method is that the probability of whether the egg will die is performed after laying even if the cuckoo egg was more fit. This means that there is a possibility koef_pa that any egg will die, no matter what lies there, just as in nature. If the egg died or was thrown out of the nest, which, in fact, is the same thing, then the nest will be free for a new laying of an egg of any fitness, even lower, which algorithmically means research in a new place.
This way one of the methods of natural evolution, such as nest parasitism, can be described in just a few lines of code. Many authors in their publications recommend to initialize the nest after removing the egg with new random values, which means starting the search from the very beginning. In most cases, this will not give the desired result in terms of increasing the exploratory ability of the algorithm. My own research has shown that it is more expedient to simply leave the nest empty and one of the cuckoos will lay an egg in it, regardless of the quality of the egg. This is better than just random values. The variability in the study is provided by random jumps in random directions from the current coordinates. As a result, we will need less iterations in search for the best solution, thereby increasing the rate of convergence of the algorithm as a whole.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::LayEggs () { int ind = 0; //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ for (int i = 0; i < cuckoosNumber; i++) { ind = (int)round (RNDfromCI (0.0, nestsNumber - 1)); if (cuckoos [i].e > nests [ind].e) { nests [ind].e = cuckoos [i].e; ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY); if (cuckoos [i].e > eB) { eB = cuckoos [i].e; ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY); } } else { ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY); } } //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv for (int n = 0; n < nestsNumber; n++) { if (RNDfromCI (0.0, 1.0) < koef_pa) { nests [ind].e = -DBL_MAX; } } } //——————————————————————————————————————————————————————————————————————————————
Here are the test results:
2022.11.30 11:31:54.490 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.918379100238852
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) Score: 1.00000
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 20 Skin's; Func runs 10000 result: 4.257477577760983
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) Score: 0.84220
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.3521208312080903
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) Score: 0.14849
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.7600394018343262
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) Score: 0.99557
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.4968964923017033
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) Score: 0.28107
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.07638950254648778
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) Score: 0.04321
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) Score: 1.00000
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 2.69
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) Score: 0.22417
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.40800000000000003
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) Score: 0.03400
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) All score for C_AO_COA: 0.507633670637353
The Levy flight cuckoo search algorithm showed impressive results. In most tests, it outperformed other optimization algorithms. In particular, the algorithm showed 100% convergence on the smooth Skin function with two variables and on the discrete Megacity function with two variables. What is even more surprising, it showed excellent scalability on a discrete function. In other tests, it is only slightly inferior to the ant colony algorithm. At the moment, we have an undoubted leader in the rating table.
I would like to clarify that all algorithms have tuning parameters that affect the final results to one degree or another, so it is quite possible that some of these algorithms have even more optimal parameters and the rating table may look different. I just showed the results of the tests with the parameters that I could find to ensure the best result. If you manage to find more optimal parameters and get better results, then I can correct the rating table based on them. There is an assumption that the ant algorithm can successfully compete with the current leader, since in some indicators it is ahead of the cuckoo search algorithm, and is minimally behind it in terms of final indicators. GWO is still a leader on the Skin function with 1000 variables. In any case, those who will use algorithms in their projects when solving their optimization problems can navigate the table and choose an algorithm for their specific needs.
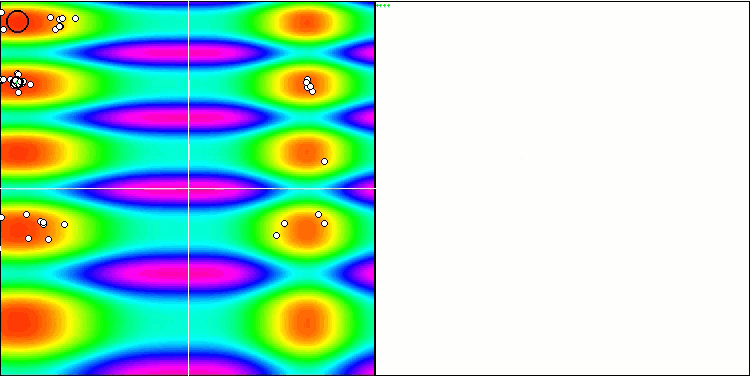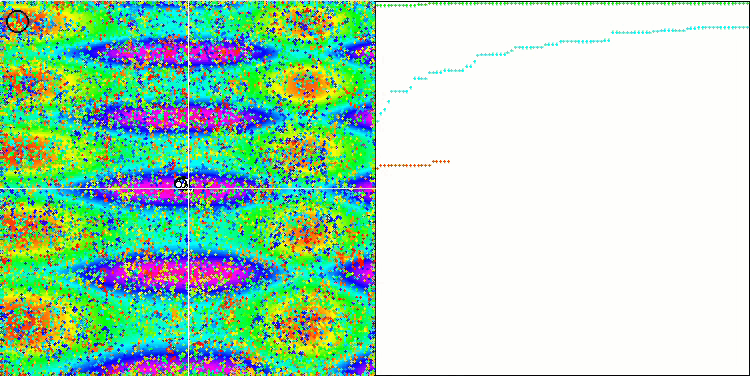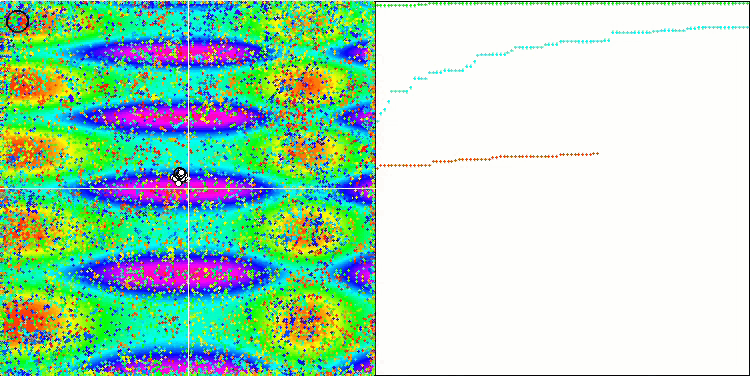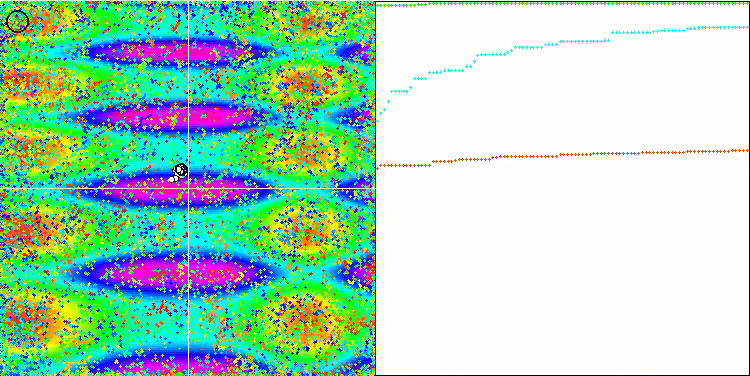
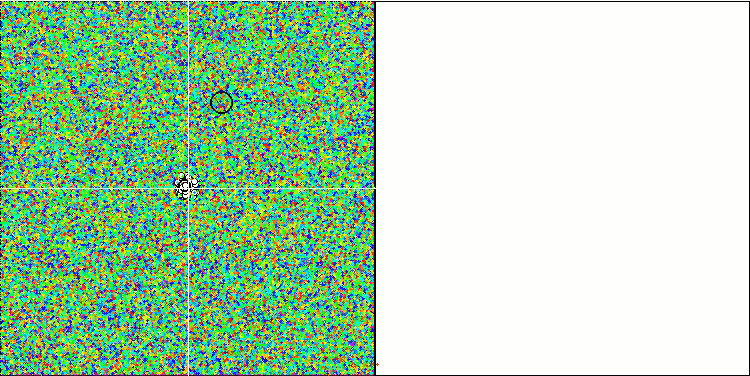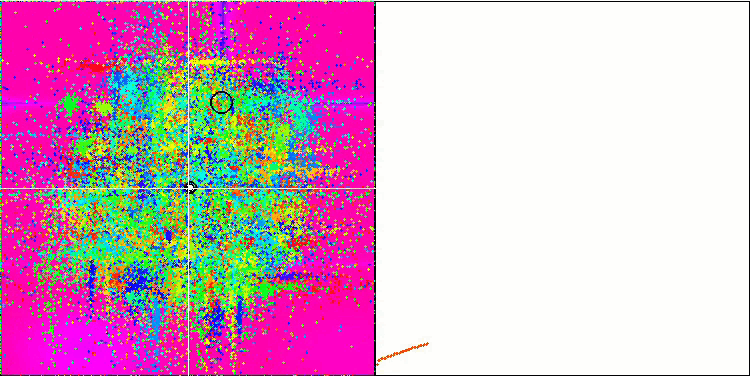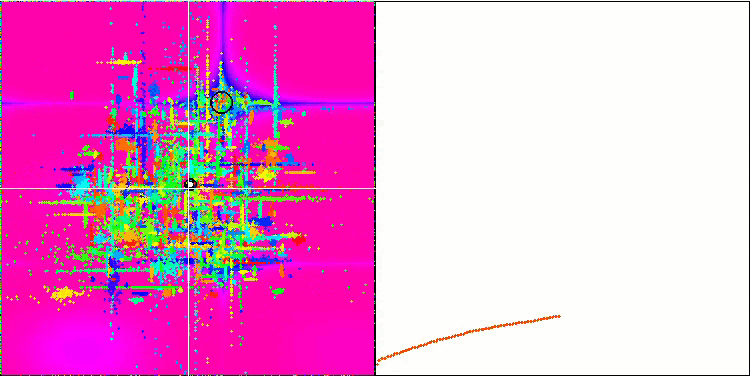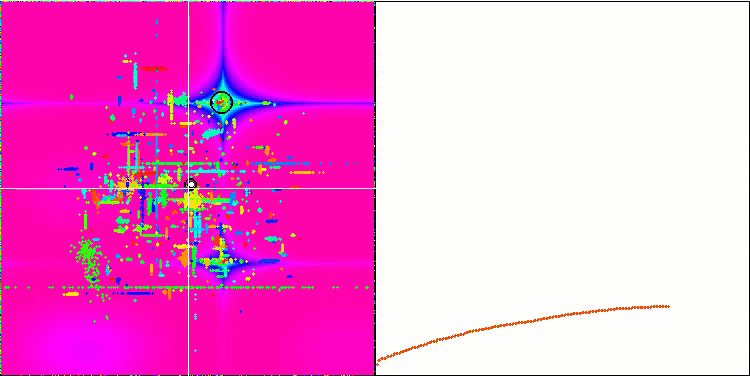
COA on the Skin test function.
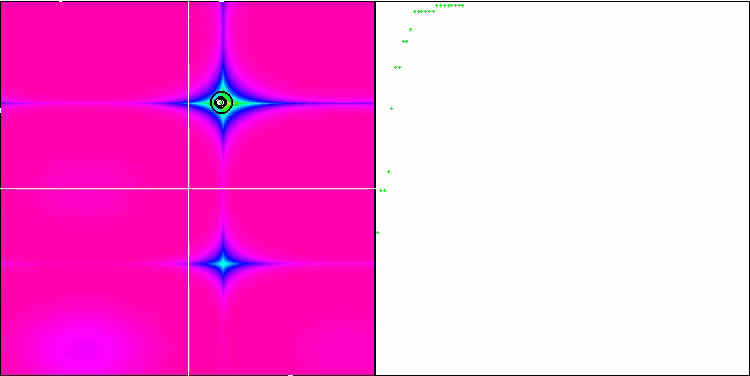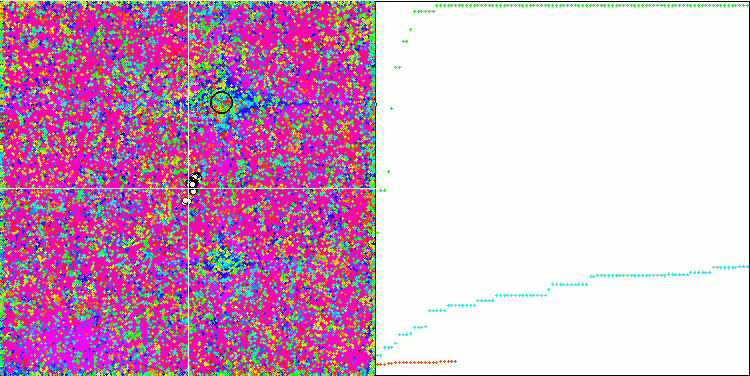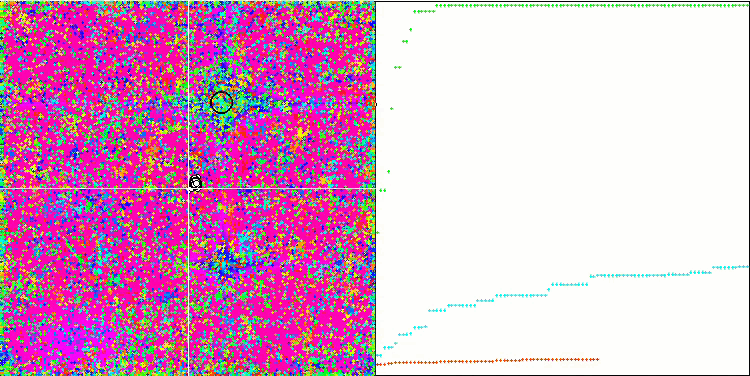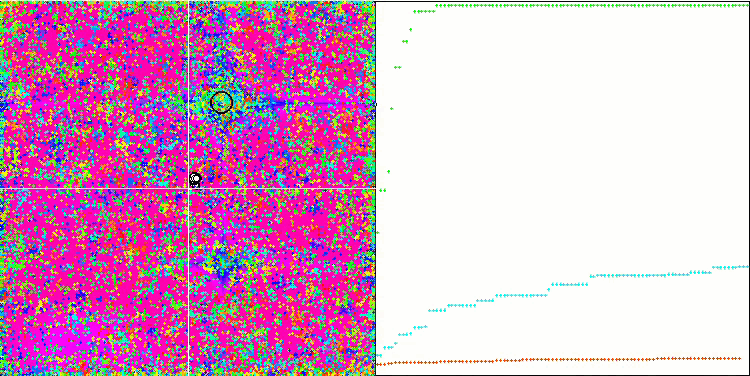
COA on the Forest test function.
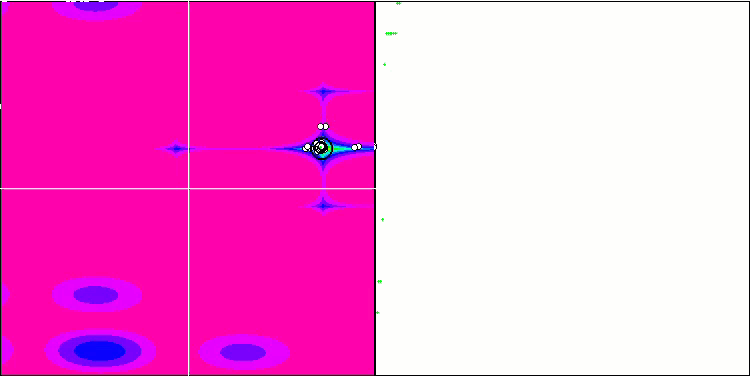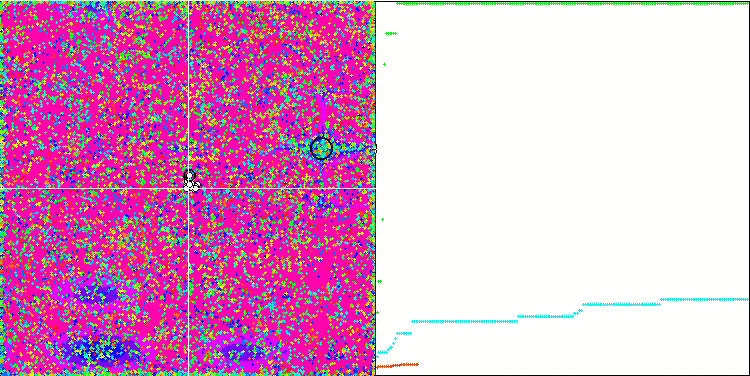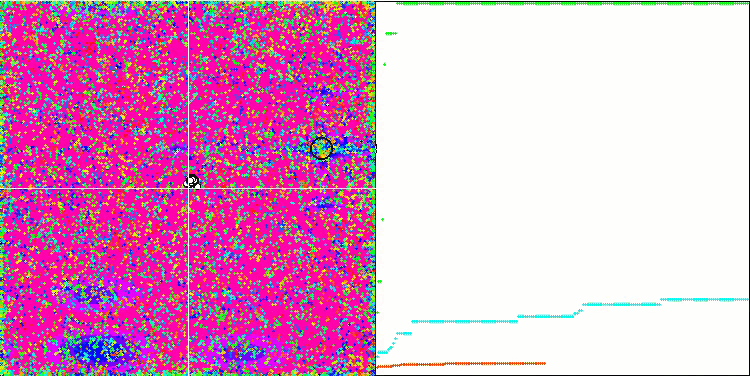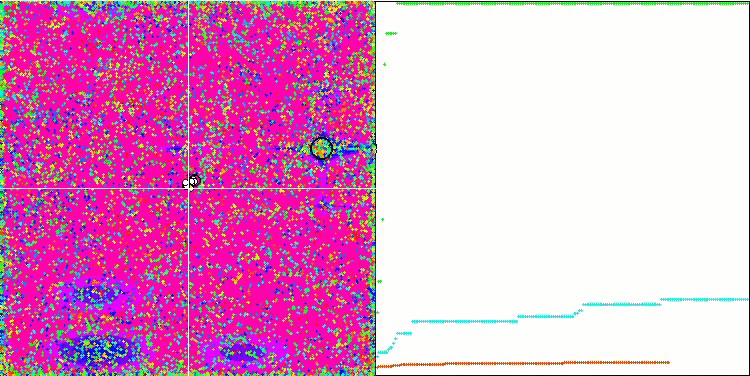
COA on the Megacity test function.
On the visualization of the test stand, the behavior of the algorithm differs from those considered earlier, however, there are some features that are characteristic of algorithms that break the task into study areas, such as the bee colony algorithm. This characterizes the ability of the algorithm not to focus on a single extremum, but to explore several potentially promising areas, providing the algorithm with resistance against getting stuck in local extrema. In this regard, it might be possible to improve the algorithm by sorting the nests and choosing among them by the cuckoo in proportion to their quality. This would mean the cuckoo choosing nests, instead of putting an egg in a randomly selected nest, as in the canonical version of the algorithm. However, this did not improve the results demonstrating the practicality of the random choice of nests. Perhaps this echoes what happens in nature. Replacing an egg in case of smarter hosts is more difficult making it randomly and statistically unjustified.
Another feature of the algorithm is that it behaves like a random walk on functions with many variables. Visually, it looks like white noise or an old TV screen. Some concentration of coordinates in the places of local extrema is noticeable only by the end of the iterations. I would like to provide a clearer "crystallization" of the parameters, as is the case with the ant colony algorithm. Thus, we have come to the general problem of all optimization algorithms, which has no general solution. Many authors of classical and fairly new algorithms have tried to solve it.
The essence of the problem is as follows: it is not known for certain which of the optimized parameters of the function under study has priority or strength, it is not known to what extent and how each of the parameters affects the result. For example, there are several parameters and the algorithm has already found the right one, but which of them exactly is unknown. The algorithm will keep trying to change all of them, although it is enough to change only a few to reach the global extreme. The problem is exacerbated when it comes to a function with many tens and thousands of variables. The more variables, the more acute the problem. Visually, this looks like white noise on the screen.
I have made an attempt to solve this problem at least partially. If it is not known a priori which of the parameters of the function under study should be changed and which should remain the same, we can try to solve this in a probabilistic way. We make the assumption that only a part of all parameters needs to be changed, and not all at the same time. The PSO algorithm behaves in a characteristic way. With an increase in the number of parameters (arguments) of the optimized function, it behaves like a cloud that does not have the ability to concentrate. To do this, I introduced a new parameter for the algorithm, which sets the probability that the coordinate will be changed, otherwise the coordinate will be left the same.
And the result is... Positive!!! The test results have improved. "Crystallization" that I wanted to achieve has appeared on functions with many variables.
The test stand results look as follows:
2022.12.03 16:01:26.256 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.918367945334852
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) Score: 1.00000
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 20 Skin's; Func runs 10000 result: 4.328327964103814
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) Score: 0.85911
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.3297901702583084
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) Score: 0.14316
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.755200932219688
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) Score: 0.99283
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.5089243656052672
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) Score: 0.28787
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.08044934398920801
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) Score: 0.04551
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) Score: 1.00000
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 2.9899999999999998
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) Score: 0.24917
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.4244
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) Score: 0.03537
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) All score for C_AO_COAm: 0.5125572342985216
We can clearly see "crystallization" on the visualization. The screen, which at first looks like white noise, is cleared, the coordinates begin to concentrate, the centers of concentration become mobile:

COAm on the Megacity test function. The effect of "crystallization" is more visible.
On the one hand, there is variability, i.e. the ability to dynamically search for new areas, while on the other hand, the ability to clarify the coordinates of already reached extremes. Below is the animation of the ant colony algorithm with a pronounced "crystallization" for comparison:
ACOm on the Forest test function.
| AO | Description | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| cuckoo optimization algorithm | 1.00000 | 0.85911 | 0.14316 | 0.99283 | 0.28787 | 0.04551 | 1.00000 | 0.24917 | 0.03537 | 0.51255778 | |
| ant colony optimization | 0.98229 | 0.79108 | 0.12602 | 1.00000 | 0.62077 | 0.11521 | 0.38333 | 0.44000 | 0.02377 | 0.49805222 | |
| artificial bee colony M | 1.00000 | 0.63922 | 0.08076 | 0.99908 | 0.20112 | 0.03785 | 1.00000 | 0.16333 | 0.02823 | 0.46106556 | |
| artificial bee colony | 0.99339 | 0.73381 | 0.11118 | 0.99934 | 0.21437 | 0.04215 | 0.85000 | 0.16833 | 0.03130 | 0.46043000 | |
| grey wolf optimizer | 0.99900 | 0.48033 | 0.18924 | 0.83844 | 0.08755 | 0.02555 | 1.00000 | 0.10000 | 0.02187 | 0.41577556 | |
| particle swarm optimisation | 0.99627 | 0.38080 | 0.05089 | 0.93772 | 0.14540 | 0.04856 | 1.00000 | 0.09333 | 0.02233 | 0.40836667 | |
| random | 0.99932 | 0.44276 | 0.06827 | 0.83126 | 0.11524 | 0.03048 | 0.83333 | 0.09000 | 0.02403 | 0.38163222 | |
One advantage of the cuckoo search algorithm is that its global search uses flights or a Levy process rather than standard random walks. Since Levy flights have infinite mean and variance, COA can explore the search space more efficiently than standard Gaussian process algorithms. Levy flight: A random walk process characterized by a series of instantaneous jumps selected from a probability density function that has a power law tail.
At the moment, the algorithm is the leader of the table significantly outperforming other algorithms in individual tests and remaining not far behind in other "disciplines". There are excellent results on the Megacity discrete function with 1000 arguments making cuckoo search a great tool for traders' tasks (that are discrete in most cases). Excellent (but not the best) results for the Skin function with 1000 arguments give reason to assert that the algorithm is suitable for training neural networks in particular and machine learning in general