Matrices and vectors in MQL5: Activation functions

Introduction

A huge number of books and articles have already been published on the topic of training neural networks. MQL5.com members have also published a lot of materials, including several series of articles.

Here we will describe only one of the aspects of machine learning — activation functions. We will delve into the inner workings of the process.

Brief overview

In artificial neural networks, a neuron activation function calculates an output signal value based on the values of an input signal or a set of input signals. The activation function must be differentiable on the entire set of values. This condition provides the possibility of error backpropagation when training neural networks. To backpropagate the error, the gradient of the activation function must be calculated - the vector of partial derivatives of the activation function for each value of the input signal vector. It is believed that non-linear activation functions are better for training. Although the completely linear ReLU function has shown its effectiveness in many models.

 

Illustrations

The graphs of the activation function and their derivatives have been prepared in a monotonically increasing sequence from -5 to 5 as illustrations. The script displaying the function graph on the price chart has been developed as well. The file open dialog is displayed for specifying the name of the saved image by pressing the Page Down key.

 

The ESC key terminates the script. The script itself is attached below. A similar script was written by the author of the article Backpropagation neural networks using MQL5 matrices. We used his idea to display the graph of the values of the corresponding activation function derivatives together with the graph of the activation function itself.

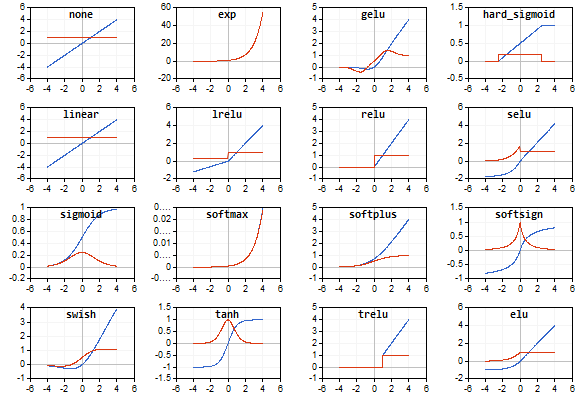
The activation function is shown in blue, while the function derivatives are displayed in red.

 

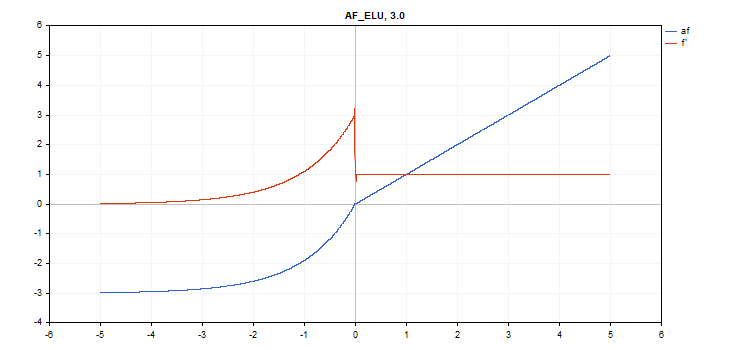
Exponential Linear Unit (ELU) activation function

Function calculation

   if(x >= 0)
      f = x;
   else f = alpha*(exp(x) - 1); 

 

Derivative calculation

   if(x >= 0)
      d = 1;
   else d = alpha*exp(x); 

This function takes an additional 'alpha' parameter. If it is not specified, then its default value is 1.

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter 

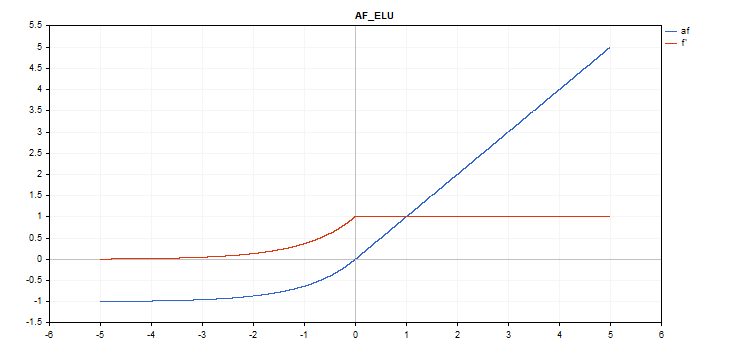
   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

 

 

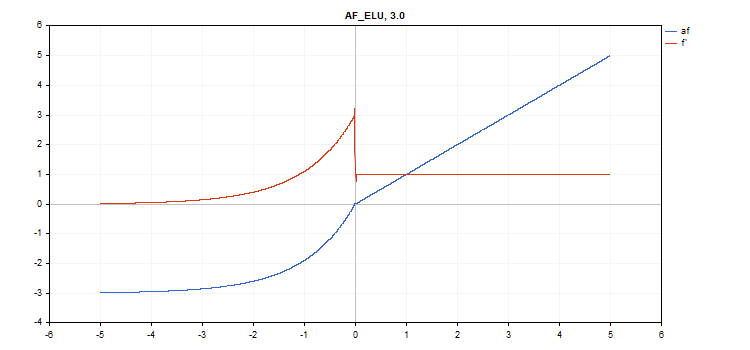
Exponential activation function

Function calculation

   f = exp(x); 

The same exp function serves as a derivative of the exp function.

As we can see in the calculation equation, the Exponential activation function has no additional parameters

vector_a.Activation(vector_c,AF_EXP);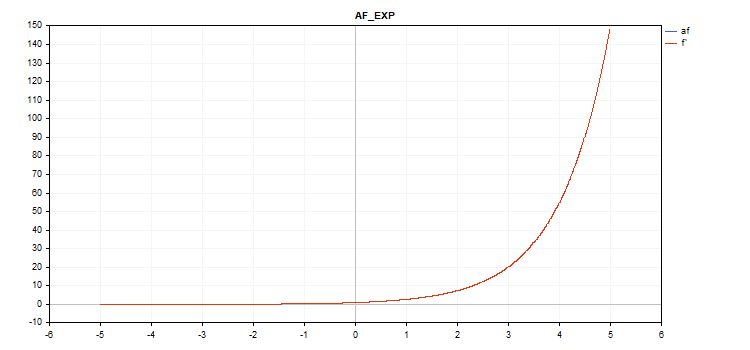

 

Gaussian Error Linear Unit (GELU) activation function

Function calculation

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3))); 

Derivative calculation

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5; 

No additional parameters.

vector_a.Activation(vector_c,AF_GELU);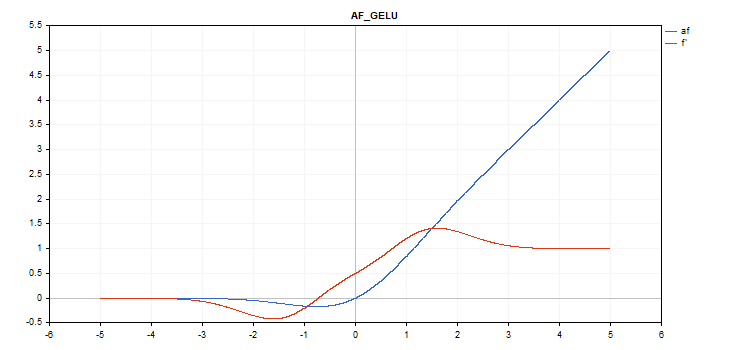

 

Hard Sigmoid activation function

Function calculation

   if(x < -2.5)
      f = 0;
   else      {
      if(x > 2.5)
         f = 1;
      else          f = 0.2*x + 0.5;
     } 

Derivative calculation

   if(x < -2.5)
      d = 0;
   else      {
      if(x > 2.5)
         d = 0;
      else          d = 0.2;
     } 

No additional parameters.

vector_a.Activation(vector_c,AF_HARD_SIGMOID);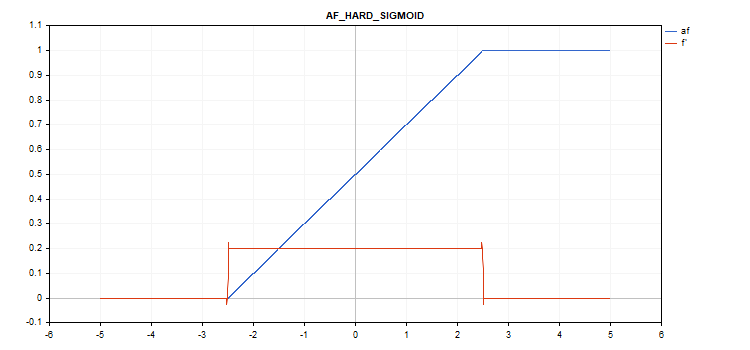

 

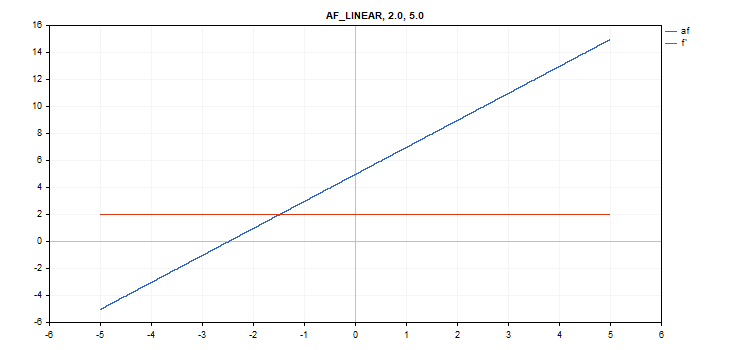
Linear activation function

Function calculation

   f = alpha*x + beta

Derivative calculation

   d = alpha

Additional parameters alpha = 1.0 and beta = 0.0

vector_a.Activation(vector_c,AF_LINEAR);       // call with default parameters

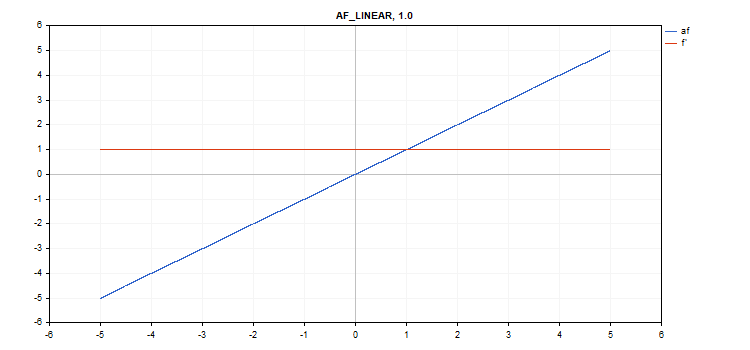
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

 

 

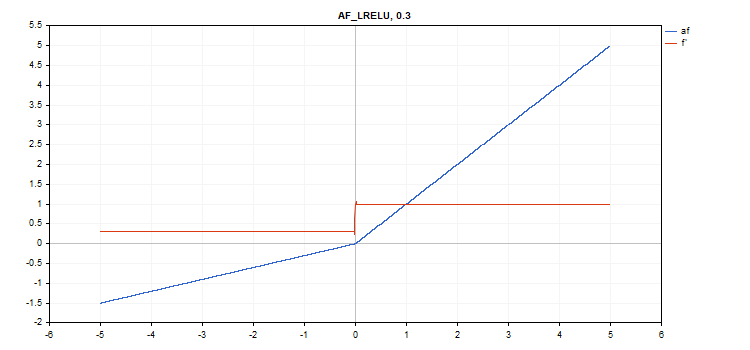
Leaky Rectified Linear Unit (LReLU) activation function

Function calculation

 if(x >= 0)
      f = x;  else       f = alpha * x; 

Derivative calculation

 if(x >= 0)
      d = 1;  else       d = alpha; 

This function takes an additional 'alpha' parameter. If it is not specified, then its default value is 0. 3

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter 

 

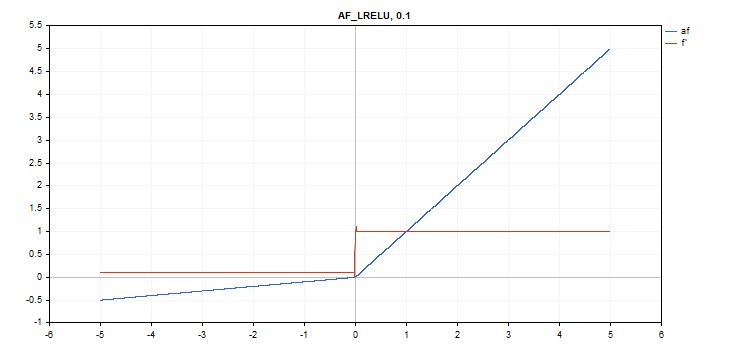
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

 

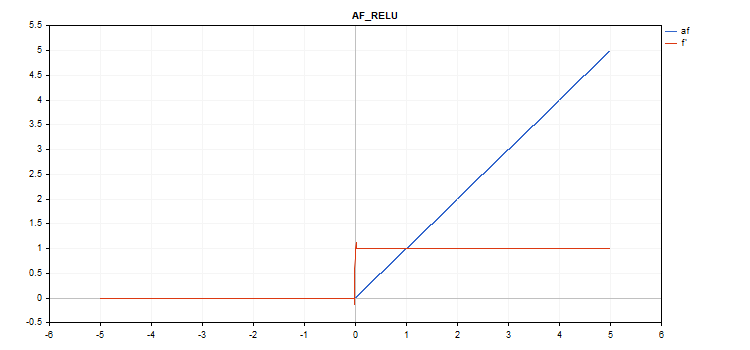
Rectified Linear Unit (ReLU) activation function

Function calculation

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else          f = 0;
     }
   else      {
      if(x >= max_value)
         f = x;
      else          f = alpha * (x - treshold);
     } 

Derivative calculation

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else          d = 0;
     }
   else      {
      if(x >= max_value)
         d = 1;
      else          d = alpha;
     } 

Additional parameters alpha=0, max_value=0 and treshold=0.

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

 

vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

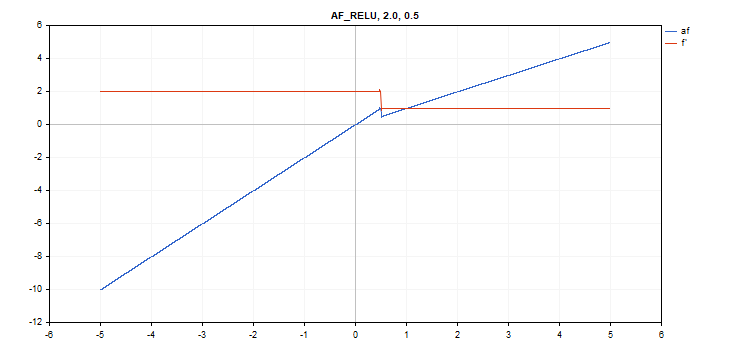
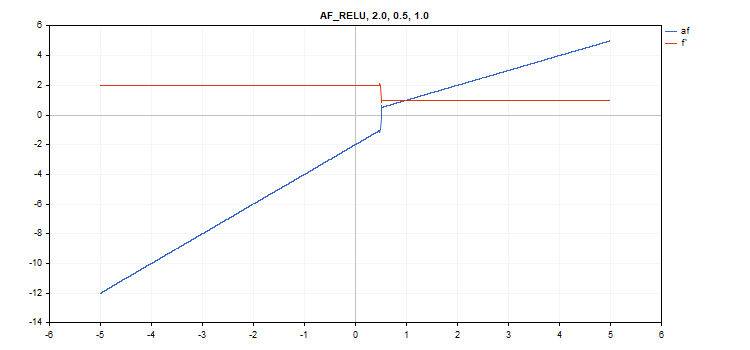
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

Scaled Exponential Linear Unit (SELU) activation function

Function calculation

   if(x >= 0)
      f = scale * x;
   else       f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324 

Derivative calculation

   if(x >= 0)
      d = scale;
   else       d = scale * alpha * exp(x); 

No additional parameters.

vector_a.Activation(vector_c,AF_SELU);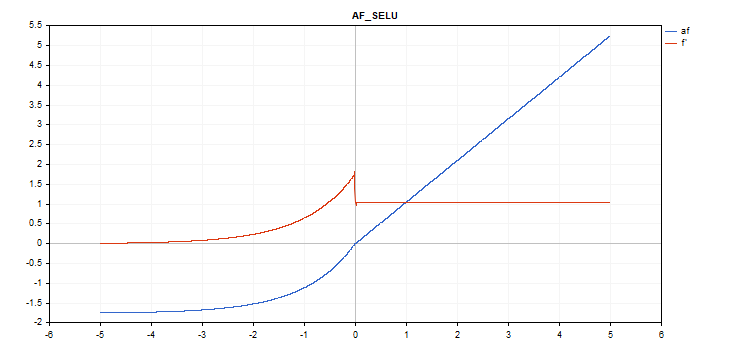

Sigmoid activation function

Function calculation

   f = 1 / (1 + exp(-x));

Derivative calculation

   d = exp(x) / pow(exp(x) + 1, 2);

No additional parameters.

vector_a.Activation(vector_c,AF_SIGMOID);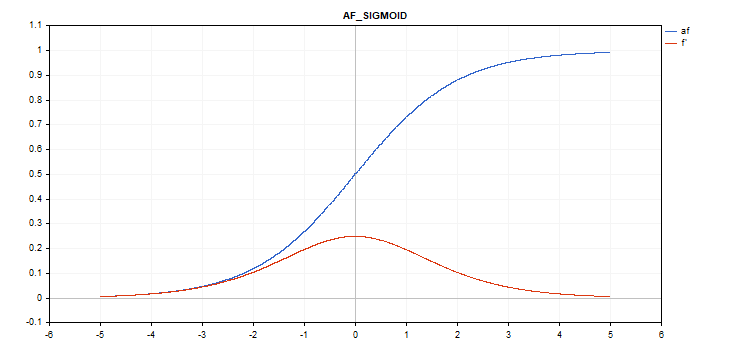

 

Softplus activation function

Function calculation

   f = log(exp(x) + 1);

Derivative calculation

   d = exp(x) / (exp(x) + 1);

No additional parameters.

vector_a.Activation(vector_c,AF_SOFTPLUS);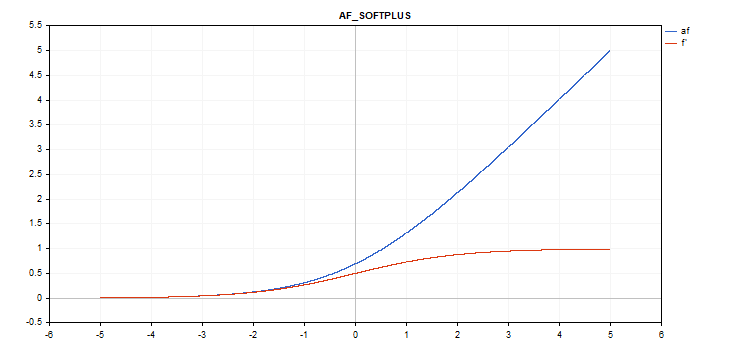

 

Softsign activation function

Function calculation

   f = x / (|x| + 1)

Derivative calculation

   d = 1 / (|x| + 1)^2

No additional parameters.

vector_a.Activation(vector_c,AF_SOFTSIGN);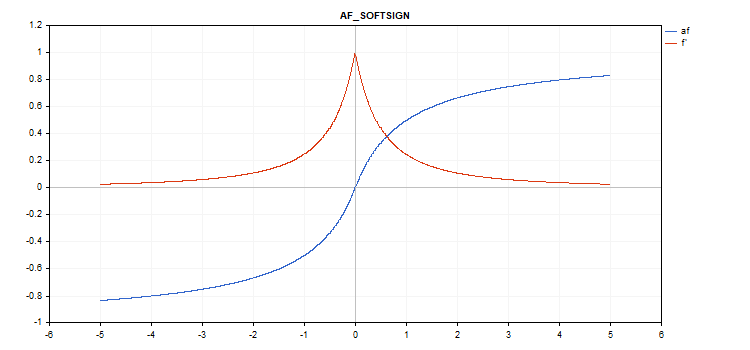

 

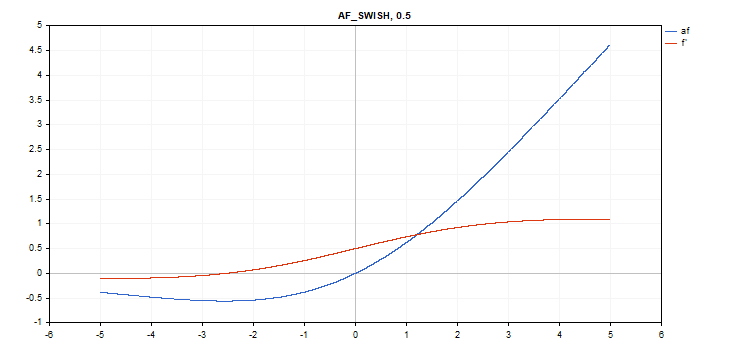
Swish activation function

Function calculation

   f = x / (1 + exp(-x*beta));

Derivative calculation

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2); 

Additional parameter beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

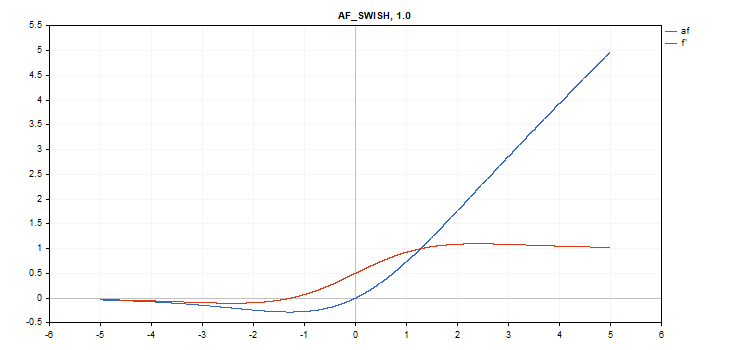
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

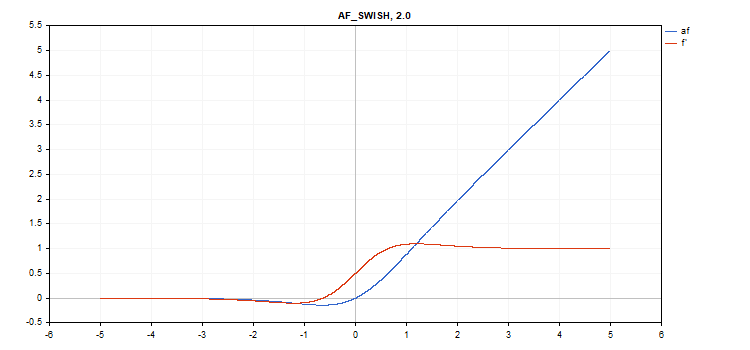
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

 

Hyperbolic Tangent (TanH) activation function

Function calculation

   f = tanh(x);

Derivative calculation

   d = 1 / pow(cosh(x),2);

No additional parameters.

vector_a.Activation(vector_c,AF_TANH);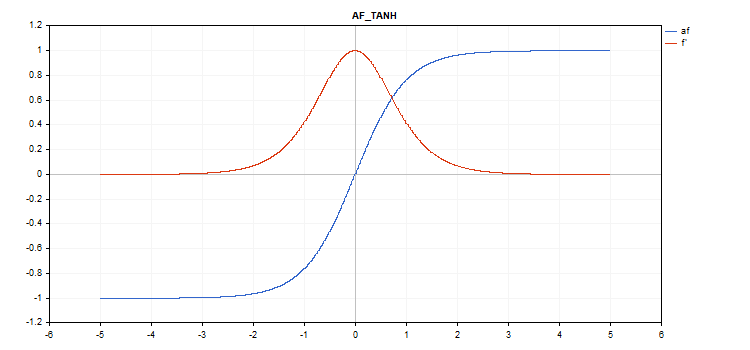

 

 

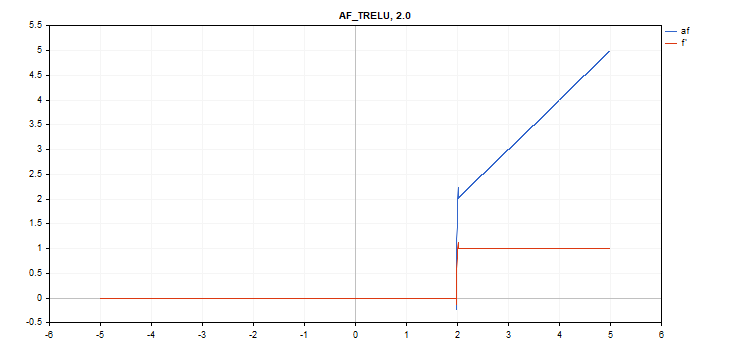
Thresholded Rectifiedl Linear Unit (TReLU) activation function

Function calculation

   if(x > theta)
      f = x;
   else       f = 0; 

Derivative calculation

   if(x > theta)
      d = 1;
   else       d = 0; 

Additional parameter theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

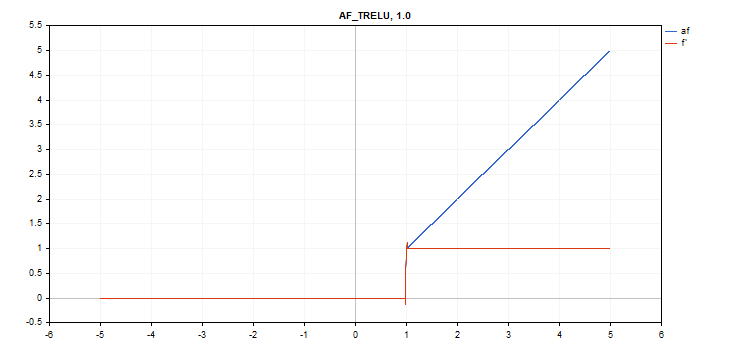
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0 

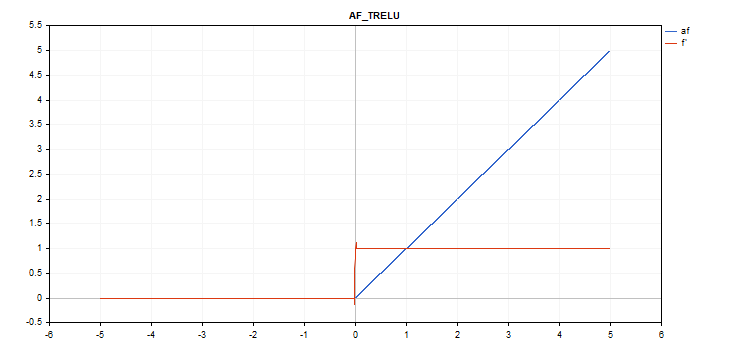
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

 

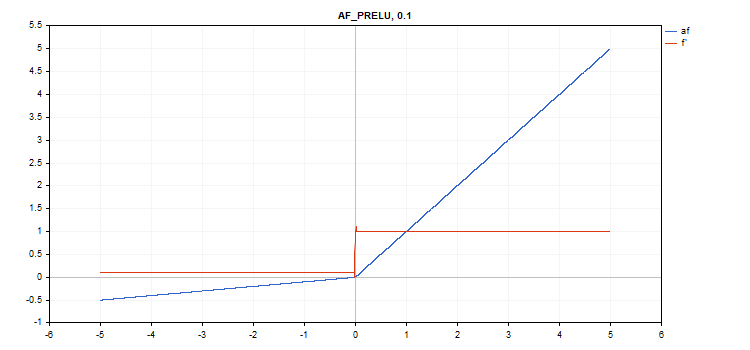
Parametric Rectifiedl Linear Unit (PReLU) activation function

Function calculation

   if(x[i] >= 0)
      f[i] = x[i];
   else       f[i] = alpha[i]*x[i]; 

Derivative calculation

   if(x[i] >= 0)
      d[i] = 1;
   else       d[i] = alpha[i]; 

Additional parameter - 'alpha' coefficient vector.

 

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha); 

 

 

Special Softmax function

The result of calculating the Softmax activation function depends not only on a specific value, but also on all vector values.

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp 

Derivative calculation

   d = f*(1 - f)

Thus, the sum of all activated vector values is 1. Therefore, the Softmax activation function is very often used for the last layer of classification models.

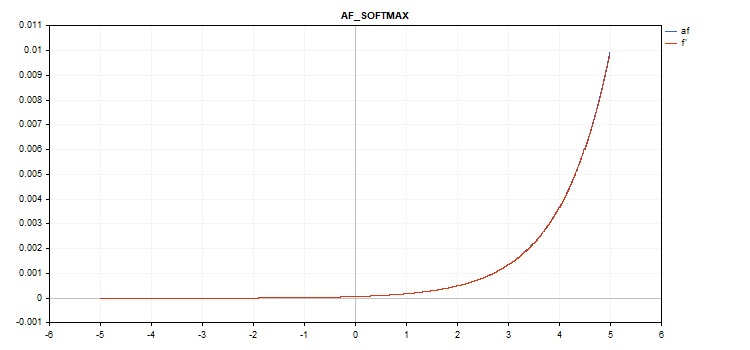
Vector activation function graph with values from -5 to 5

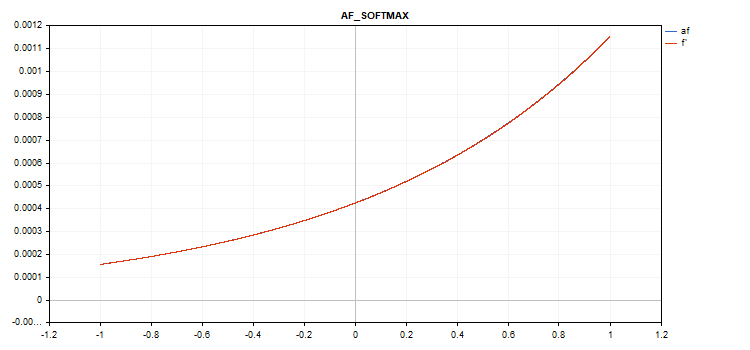
Vector activation function graph with values from -1 to 1

 

 

If there is no activation function (AF_NONE)

If there is no activation function, then the values from the input vector are transferred to the output vector without any transformations. In fact, this is the Linear activation function with alpha = 1 and beta = 0.

Conclusion

Feel free to familiarize yourself with the source codes of activation functions and derivatives in the ActivationFunction.mqh file attached below.