Monoid Groups

Monoid Groups

Introduction

In previous article we continued our look at monoids by tackling monoid-actions which we saw as a means of transforming monoid sets by expanding their possible elements. Thus far on the whole, we have covered the concepts of: domains, morphisms, category axioms, right up to, and monomorphic-pullbacks & epimorphic-pushouts. While some may argue that implementation of category theory concepts require a broader study of all/ most of its concepts, the approach taken here is to explore what ideas can be of use from a basic or limited view of the subject. Each of these articles on their own, though in some cases concepts were borrowed from prior articles, showed efficacy in facilitating trader decisions and in some cases potential to define trading systems. For this article we are going to consider monoid - groups and these like the monoid actions we covered in prior article, will be viewed as a re-definition of a monoid at a trade decision point. Recall monoid actions were seen as an extension of the monoid set, here we will be re-evaluating another monoid parameter, namely the identity element as we re-define our monoids once again. The scope of this article will not include building complete trading systems as has been the case in some previous articles where we coded instances of the expert signal and/ or expert trailing class with the goal of assembling complete expert advisors with the inbuilt MQL5-wizard. Rather we will look at individual functions that are part of our coded monoid, monoid-action, and monoid-group classes, and examine how they can be useful to a trader at key decision points.

Understanding Monoid Groups

To recap monoids are three things namely a set, an identity element that belongs to that set, and a binary operation that takes any two elements of that set and always returns an element that is a member of the set. In addition, if any members of the set are paired with the identity element in the binary operation then the output is always that element. Monoid-actions which were covered in our most recent article are a form of function, defined by a set and binary operation, that pair members of the monoid set, with this function’s set and always output an element that is a member of the function’s set. We saw them as a means of transforming a monoid because remember the output of a monoid’s binary operation was closed since all outputs were strictly members of the monoid set.

To begin though, it might be constructive to first to point out that there is no distinction per se between groups and what we are referring to as monoid-groups here. The only difference, as hinted at in the prefix ‘monoid’, is that we are strictly referring to sets (or domains), that belong to a category. A monoid group therefore, following the group definition, is a monoid with an additional property that every element in monoid set should have another element that is its inverse. When an element and its inverse are paired in the monoid binary operation, the output is always the monoid’s identity element.

Formally the inverse property that sets monoid-group

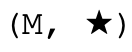
apart from regular monoids is, for every

there is also an inverse

such that:

where e is identity element of monoid.

The application of this to traders will be considered in a manner similar to what we had in the prior article. Recall we are viewing monoids (the sets) as a pool of decision options a trader may choose from and in our last article we looked at extending the size of this pool with monoid-actions. We examined what impact this had on performance of a trading system if we extended scope of particular monoids based on a list of factors that weighed relative importance of the decision points (features) of the trade-system. The results were worse-off to average compared to what we had got in the article before that which considered restricted (default) monoids. For monoid-groups, rather than expand the scope of our monoid sets we will revert to restricted monoids that have had action and are transformed to groups. We will review the change in set composition following this monoid action but the actual implementation of a trading system will not be considered for this article. That is something the reader is invited to explore independently.

Implementing Monoid Groups in MQL5

In setting up our MQL5 environment to implement monoid-groups, we’ll launch the IDE and create a new script file from the wizard.

We then name our script ‘ct_10’ on the next tab, and click finish. This script is going to refer to a class file ‘ct_10.mqh’ which will be a modification of the class we referred to in the previous article ‘ct_9.mqh’. For completeness it may be helpful to walk through the steps of creating the monoid class, which was part of ‘ct_9.mqh’, that we referred to in the previous two articles. This had been glossed over but it should be constructive going forward. Recall our basic building unit is the element class which primarily constitutes an array of objects of data type ‘T’. Data type ‘T’ is set when the element is initialized.

//+------------------------------------------------------------------+ //| ELEMENT CLASS                                                    | //+------------------------------------------------------------------+ template <typename T> class CElement                      : public CObject
   {
      protected:
      
      int                           cardinal;
      T                             element[];
      
      public:
      
      bool                          Cardinality(int Value) { ... }
      int                           Cardinality() { return(cardinal); }
      
      ...
                                    
                                    CElement(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CElement(void) {};
   };

Element class is in turn called by a set (domain class) as an array.

//+------------------------------------------------------------------+ //| DOMAIN CLASS                                                     | //+------------------------------------------------------------------+ template <typename T> class CDomain                       : public CObject
   {
      protected:
      
      int                           cardinal;
      CElement<T>                   elements[];
      
      public:
      
      bool                          Cardinality(int Value) { ... }
      int                           Cardinality() { return(cardinal); }
      
      ...
      
                                    CDomain(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CDomain(void) {};
   };

We had gone further and defined not just the category class, which ceremonially defines monoid groups as distinct from groups, but classes for morphisms, homomorphisms, and a continuum of other concepts. Because these and the category class are not critical per se to constructing the monoid class we will not list or consider them for this article. So, recall a monoid is three things namely a set, an identity element, and a binary operation. If we start by defining what a binary operation is, we could achieve this by listing our options in the form of an enumeration. We have used for the past 2 articles something that resembles this.

//+------------------------------------------------------------------+ //| Enumeration for Monoid Operations                                | //+------------------------------------------------------------------+ enum EOperations
  {
      OP_FURTHEST=5,
      OP_CLOSEST=4,
      OP_MOST=3,
      OP_LEAST=2,
      OP_MULTIPLY=1,
      OP_ADD=0   };

We will not revise this for our article but suffice it to say it does set a means by which one can customize and define what they consider to be binary operations for their respective monoid set elements. And the possibilities here are interesting. Moving on to the monoid class, rather than define a new class with a set (domain) instance, we construct our class as inheriting publicly from the domain class. This is code efficient and it also intuitively says a monoid is simply a domain with a binary operation and an identity element attached to it.

//+------------------------------------------------------------------+ //| Monoid Class                                                     | //+------------------------------------------------------------------+ template <typename T> class CMonoid                       : public CDomain<T>
   {
      protected:
      //double                        weights[];       
      int                           identity;
      EOperations                   operation;
      
      public:
      
      double                        weights[];
      
      ...
      
      void                          Operation(EOperations Value) {  operation=Value; }
      EOperations                   Operation() { return(operation); }
      
      ...
      
                                    CMonoid(){ identity=0; operation=OP_ADD; };
                                    ~CMonoid(){};
   };

To this class we than add the two extra axioms of a binary operation and identity element. Our identity element though, is not another instance of an element as that would be repetitive since it is already in the array of elements of the domain. Rather we simply refer to an index of that array as pointing to our identity element. The monoid class can be initialized by automatic pointer in our script as shown in example below.

The monoid actions covered in the last article had their class inherit from this monoid class.

For monoid groups though, semantically there is no difference in class code between a monoid and a monoid group. The requirement for inversion with monoid groups can only be checked. So, for our purposes the monoid group class will feature an ‘HasInversion’ check function as shown below.

//+------------------------------------------------------------------+ //| Monoid Group Class                                               | //+------------------------------------------------------------------+ template <typename T> class CMonoidGroup                 : public CMonoid<T>
   {
      protected:
      
      public:
      
      bool                          HasInversion() 
                                    {  
                                       bool _has_inversion=true;
                                       
                                       for(int i=0;i<this.Cardinality();i++)
                                       {
                                          bool _has_inverse=false;
                                          
                                          for(int ii=0;ii<this.Cardinality();ii++)
                                          {
                                             if(Operate(i,ii)==Identity()){ _has_inverse=true; }
                                          }
                                          
                                          if(!_has_inverse){ _has_inversion=false; break; }
                                       }
                                       
                                       return(_has_inversion); 
                                    }
      
                                    CMonoidGroup(){};
                                    ~CMonoidGroup(){};
   };

Now in the previous two articles elements of monoid and monoid-action class could and did constitute none normalized data. Meaning prior to use in the binary operations they had to be converted to a format that allowed equitable comparison. This format in this article will be called weights. In the previous articles these weight values were calculated and used at run time. Here we are going to have the monoid-group class introduce parameters to set, store, and get the values of these weights within the class. All weights will be double data type.

      CMonoidGroup<int> _vg;        //valid inversion group       CMonoidGroup<int> _ig;        //invalid inversion group       
      _vg.Weights(5);             //set group size       _ig.Weights(5);             //set group size       for(int i=0;i<5;i++)
      { 
         CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2);
         _vg.Set(i,_ve,true);      //set element          _vg.SetWeight(i,double(i-2));  //set weight          
         CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i);
         _ig.Set(i,_ie,true);      //set element          _ig.SetWeight(i,double(i));   //set weight       }
      
      _vg.Operation(OP_ADD);      //set monoid operation to add       _vg.Identity(2);            //set identity element index to 2       
      _ig.Operation(OP_ADD);      //set monoid operation to add       _ig.Identity(2);            //set identity element index to 2 as above or any index       
      printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. ");
      ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
      
      printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. ");
      ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);

To see this code in action let us create an instance of the monoid group, and run print checks with our class functions to see what output we get. What our code whose complete listing is attached to this article, is simply confirming inversion within a set. Every element should have an inverse about the identity element.

2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights. 2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2 2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights. 2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4 

For practical purposes the monoid group ‘_vg’ was given a size of 5 but its actual size is unlimited since to match all the axioms of a group any pairing on numbers in the binary operation should always result in a number that is a member of the group set. With what we have used pairing two and one will result in three which is not listed in the set. So ‘_vg’ is an unbound set of integers (Z).

Uses of Monoid Groups in Algorithmic Trading

In the prior two articles, since we started looking at monoids we have taken them as decision points. Specifically, they have been used in deciding on:

-length of the look-back analysis period to consider;

-time frame to use;

-applied price to use;

-indicator to use;

-and, trade method to engage (whether trend following, or counter trend).

In making them decision points, the sets of each of these monoids constituted the options a trader could be faced with. What was not clearly mentioned in these articles, though it was implemented, was the weighting of each element in the monoids’ respective sets. Prior to carrying out the monoid binary operations across all set elements in order to make a selection, the set elements needed to be normalized. In some cases, like with applied price for instance, it was not easy to make comparisons on a price bar by price bar basis which is what some trade situations demand. We therefore had to find a way of quantifying these set elements in a way that would adapt as the price action, or whatever basis metric was chosen, changed with time. So, this ‘quantification’ of the set elements is what we will refer to as weights for this article.

Now for the application, after weighting our element values, in order to use groups, we would need to apply the ‘OperateModulo’ function in the revised monoid action class, since the last articles. The actual group set that is in our action class is not listed since it is simply a list of integers up to a size defined by our inputs to the script. What is logged is a relative set to this group since modulo action on the initial set is bound to yield repetitions.

And this is how the ‘Operate’ function would implement this, as a method with the monoid action class.

      int                           OperateModulo(int Index,int Modulo=1)
                                    {
                                       int _operate=-1;
                                       
                                       if(Index>=0 && Index<this.Cardinality())
                                       {
                                          int _value=int(round(set.weights[Index]));
                                          
                                          _operate=_value%Modulo;
                                       }
                                       
                                       return(_operate);
                                    }

So once our monoid sets are transformed to a smaller ‘circular’ set, the binary operation for this smaller monoid on pairing any two elements can output the one furthest from the identity element where in our case the identity element will always be the middle index. Setting the size of the monoid group requires the size is an odd number.

If two elements are equidistant from the identity then the identity element is chosen. So, to recap our monoid action here is effectively normalizing the base monoid set into a group. We would then make our decision from pairing the elements based on their value in the monoid action set, with the monoid action binary operation.

Since we are not coding and testing an expert advisor for this article, for illustration of the outputs of monoid groups, at each of our five afore mentioned features, we will print the monoid set with the options a trader is facing, the weights to which these set values get converted, the monoid action values on these weights that yield monoid group values, and the relative set of this monoid group. Notice we are referring to relative sets again since an earlier article, that is because in order to have the set of the monoid action as a group we will use modulo off an input size to normalize and fit all the values of our weights into an action set which will also be a group. In normalizing these values with modulo we are bound to have repetitions which is why the action set is strictly not a group but a relative set to a group whose members simply constitute all the integers starting from zero up to the input size minus one.

Our print logs will conclude at the elements of the action set which is relative to a group as mentioned above. It is then up to the reader to carry forward the computed values in each action monoid from the time frame monoid up to the decision monoid by making selections following the axioms of groups outlined above. Just to reiterate in a group set binary operations, just like monoids, if any of the paired elements is the identity non-identity element is the output, and in addition if paired elements are inverses to each other, then output will be identity element.

In addition, it may be insightful to make selections starting with timeframe then look back period as opposed to what we considered in the previous two articles. With that said, this is how we will get our weights for the time frame monoid.

//+------------------------------------------------------------------+ //|                                                                  | //+------------------------------------------------------------------+ void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G)
   {
      for(int i=0;i<G.Cardinality();i++)
      {
         ResetLastError();
         int _value=0;
         ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true);          if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3)
         {
            _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close))));
         }
         else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); }
         
         ResetLastError();
         if(!G.SetWeight(i,_value))
         {
            printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
         }
      }
   }

Notice all weighting will now be normalized to integer format because we want to use modulo in converting it, by monoid action, into a set relative to a group. So, for our time frames since weighting had been a positive double that was never more than one we will have this converted to an integer that can be any value from 0 to 10,000. Also, our input size parameter for time frames, with default at 51, will the value we use to get the remainder, a member of the group set. Remainder values are stored in the weights array of the monoid-action class.

So, if we attach our script to the chart of USDJPT on the one-minute timeframe, as of some time on 15.06.2023, this was the output for the timeframe monoid.

2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130 2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)} 2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20 

We are using a slightly modified set of time frames from our past articles. Again, it is up to you to choose a band of timeframes that what best for what you are studying. If we run logs for look back monoid, below would be our prints.

2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4 

The prints above assume one-hour timeframe was selected at timeframe monoid. To repeat the actual final selection at each monoid, following group axioms, is not implemented in this article or attached code. This is left up to the reader to explore and take this first step in monoid groups, to the direction they feel works best with their strategy. For the applied price prints, we would have the logs below, if we took it that a look back period of 8 was chosen.

2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)} 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20 

Conclusion

We have looked at what monoid groups are by introducing the concept of symmetry to a typical monoid where we add the additional axiom that all members of a monoid group need to have an inverse and also binary operations between mirror elements are restricted to always output the identity element of the monoid group. This has been a follow up from our last article where we considered monoid actions.

We have hinted at how Monoid groups can be resourceful to traders in constrained monoid sets like we had in a previous article. In that article we took monoid sets to be a fixed-pool of a trader’s choices at a given stage. This is different from the avenue of monoid actions we took in the last article where we looked to explore the impacts of expanding select monoid sets on trade performance.

By only ‘hinting’ at the potential of monoid groups and not show casing expert advisor(s) using them as we have in the previous two articles the reader is invited to take this material further by implementing selections at each monoid following the rules of groups which we have mentioned but not coded.

In our next article we will tackle another concept of category theory.